함수 설명
관측된 시계열에 자기회귀누적이동평균모형(Autoregressive Integrated Moving Average Model)을 구축하는 데 유용한 함수를 요약하면 다음과 같다.
arima()ARIMA모형의 차수 \(p\) 와 \(q\) , 차분 수 \(d\) 를 지정하여 모형 구축
auto.arima()모형의 차수 지정없이 자동적으로 최적화된 모형 구축
acf()상관도표그림
pacf()부분상관도표그림
Box.test()Ljung-Box Test
checkresiduals()잔차가 백색잡음과정의 가정을 만족하는지 확인할 때 사용
forecast()예측
Random Walk and Momentum Plot
# AR(1)과정을 따르는 시계열 생성 set.seed (4631 )<- arima.sim (n = 500 , # 생성하고자하는 시계열 개수 list (ar = c (0.4 ))) # AR(1)과정 : Y_t = 0.4Y_{t-1}
Time Series:
Start = 1
End = 500
Frequency = 1
[1] -0.912343409 -1.701603284 1.309603454 0.691301009 0.832229499 0.555481039 -0.026684342 -0.362545410 0.693315964 -0.075195230 0.122254548 -0.370393783 -0.254577654 0.187517312 -1.708057556
[16] 0.986697733 -0.640294098 -0.885591883 -0.993104578 -0.135172972 -0.194449428 -0.123467230 -1.216275158 -0.931739467 0.031253153 -1.499635290 1.319634259 2.398330132 -0.229766437 1.332681837
[31] 0.157756638 -0.103097574 -0.102247983 2.536262232 3.218027097 0.445937187 -0.177490207 -1.602786627 -0.913088486 -1.406607759 0.099831368 -1.448052841 0.277834307 0.308540220 0.604106907
[46] 0.372668105 1.287859364 1.821393863 3.624531543 0.972845982 -0.896416641 -1.777569846 -0.695491554 -1.375497500 1.007413097 1.142459616 0.721150425 -0.400368442 -0.961452076 -0.969140832
[61] -1.968814756 -0.798978245 -1.022224506 -1.673391629 -0.705015657 0.731069223 -0.427970435 1.303036486 1.862548515 0.017150757 1.279744874 1.015345454 2.535688480 1.043884770 1.103283049
[76] 2.050819678 0.166049018 1.325027055 0.982567526 -1.866691371 -1.395834381 -2.988217256 -0.158685151 -0.491788055 -0.277597713 1.604608492 0.982089512 0.125541809 0.635742936 -0.235507928
[91] 0.132245190 -0.483377174 0.351436414 2.254957441 -0.203113635 1.751899755 1.201800038 2.079376478 1.641068416 0.012711375 0.455767972 -0.247430434 -0.419432042 -1.387682589 -0.806270199
[106] -1.412385197 -1.392636594 1.346065579 0.313476772 0.845857651 0.029078760 0.054460112 -0.885253382 -0.146332643 -0.618382418 -0.920818943 -0.338097474 -0.752403660 -1.223742893 0.689190649
[121] 0.539929591 1.258735015 0.022750117 -0.869336438 -0.828436846 -2.166858885 0.273965986 -1.037722970 -0.589593679 1.943031697 0.861840955 -0.520984536 0.770711156 1.101170054 0.846006091
[136] -2.173509959 -1.102412181 0.596310901 -0.281340324 0.879172771 -0.409098649 1.747917946 0.444448222 -0.304067456 -0.970378141 -0.237309951 -0.342986461 -0.497046979 -0.938379568 -0.230699307
[151] -0.696098707 -0.528535492 1.179030894 1.775753907 0.135886565 0.219726895 1.743976297 3.234301835 0.144757587 -1.026764175 -1.290638719 -0.293860740 0.213341896 0.656327137 0.115984113
[166] 1.718136766 0.476141379 -0.987470475 -1.852852123 -2.641018085 -0.024482023 0.491991907 0.975704783 -0.002667929 -0.136539414 -0.081797455 -0.702349988 -0.149531603 0.467953220 0.075355046
[181] -0.558518159 0.281974471 -0.899797597 -1.328805544 -0.027818037 0.802736204 -0.968890576 -0.312796925 0.867650846 -0.257391157 0.172430824 -0.313593354 1.450511226 0.445832929 -0.349042275
[196] -2.148408416 -0.898881311 0.151759003 -2.266476419 0.117458198 1.766492454 -0.526284231 0.066299695 -0.566873492 0.965266585 1.037151790 -1.587680491 1.813497932 1.255998632 0.161051227
[211] 3.054247824 0.952734586 0.452260141 0.203109914 -0.612809154 -1.421695279 -0.075559582 -0.150847637 -0.294898135 -0.191676540 -0.984143939 -0.954974484 -1.952447346 -0.407105502 -1.010789331
[226] -0.376014894 -0.639076989 -1.140124930 0.607587073 0.094643343 1.277664446 1.289747945 0.765406149 0.965295215 0.768660214 2.119481591 1.975781515 1.218813681 0.168313822 0.299093643
[241] 1.074462951 0.832784873 2.086258930 0.916655229 -0.164630750 -1.621972456 -1.146651373 -1.195654157 -0.949149364 0.278622989 -0.349154803 -0.063271529 0.487016245 -0.256592989 -0.198698480
[256] 0.139972608 -1.401984577 -0.451456758 0.546480685 -0.118633637 0.834943293 1.232088158 -0.628640225 -1.307409713 -1.459409232 -0.035619335 -0.178265267 0.126249921 -1.136784165 -2.529288363
[271] 0.386093595 0.625958961 -1.444598418 -0.757761283 -0.958362055 -1.367402052 0.002037527 0.624906595 -1.513101287 0.318593880 0.341663053 0.750263380 -1.475926277 -0.157797771 -0.245202005
[286] -0.537848659 0.110833231 -1.759603329 -0.086328201 -0.127624951 -0.587355815 -2.306925358 -0.187697381 -1.456423114 -0.186679580 -0.190593254 0.446225486 -0.710882725 0.669572420 -1.652750327
[301] -2.254961336 -0.242182465 0.667217541 0.935181469 1.634818270 0.312140714 -1.067727411 0.416256545 0.597315306 -2.083217594 -0.686914533 1.523376113 -0.589944868 0.809860833 -0.978598351
[316] -2.291625802 -0.468682911 -1.008714414 -1.689834548 -0.417147451 -0.803271601 -0.832076120 0.065363742 -0.093893644 -1.049059664 -1.444510947 -1.076551021 0.159225511 0.899011492 0.495151288
[331] -2.182210398 -0.704122441 -1.850799443 -0.911979956 -0.364270108 0.833332861 0.886993545 0.118737971 -0.608727843 -1.085932642 0.539806089 1.230683997 1.145261304 0.979793271 0.981000516
[346] 0.858859490 0.425712618 1.451944450 1.040442611 1.270852691 0.001724409 0.104234966 -0.341138452 -1.138528598 -1.618354797 -1.699497595 -0.243076411 -0.651603385 1.343148562 -1.751853045
[361] -2.139267445 -1.229228556 0.255161099 1.813250189 1.862858137 0.208573786 0.501641144 -1.252334702 -1.172962682 -1.129589843 -0.067739846 -0.062815505 -1.508314314 -0.335414905 -0.353518485
[376] 0.208172483 0.262092705 0.531750971 -0.824122936 0.017032118 -1.015173764 0.365974862 -1.400376808 -1.443808435 -0.451407292 0.066326783 -0.895822894 0.900912062 -0.037442219 -0.456481687
[391] 2.377575658 2.430206896 -1.619430146 0.987079742 0.281160126 -1.018931312 -0.794530108 1.494620796 1.388568007 -0.936099757 -1.617907620 -1.593275135 -0.836974326 -0.798359722 -1.113207216
[406] 0.511917371 -1.735132035 0.177605755 -1.184768329 0.188680990 -0.878350456 -0.586789699 -0.784074820 0.617449054 2.593695064 0.547644160 -1.303269875 0.256800524 -0.885652387 -0.367378463
[421] -0.458222229 0.632855057 -2.123028093 -0.601463044 -1.402681000 -1.015006105 0.672074035 0.441082153 0.108044662 1.241146031 0.182850562 0.532864396 2.021748358 1.453454116 -0.351721426
[436] -0.760864939 -0.342109875 0.709747073 0.678984727 -0.345892776 1.049415015 1.099538689 0.931988534 -0.307293897 0.324674165 1.332195826 0.397157781 0.460074576 0.722534790 0.911401034
[451] 1.052024961 -0.770966223 -1.270573476 0.567950193 0.663503429 1.895802731 0.792548728 0.743382531 0.966190659 -1.038656980 -0.638670844 -0.815864620 0.311205909 0.085439372 1.169179615
[466] 0.045130403 1.334452836 2.056890984 0.061869779 0.993814932 -0.051180302 0.181854157 -0.867732369 -1.729196924 -1.068033410 -1.336379582 -2.486448663 -0.743950909 -0.780466420 0.422205583
[481] -0.603969049 -1.086293175 -2.017387073 -2.463539252 -1.517367558 -1.439320711 0.757130325 1.029261284 -1.059658946 -0.542882678 0.053945454 0.336157628 -0.645807708 0.372731417 2.163157158
[496] 1.349402356 0.636951690 1.163041710 2.250858491 -0.545616025
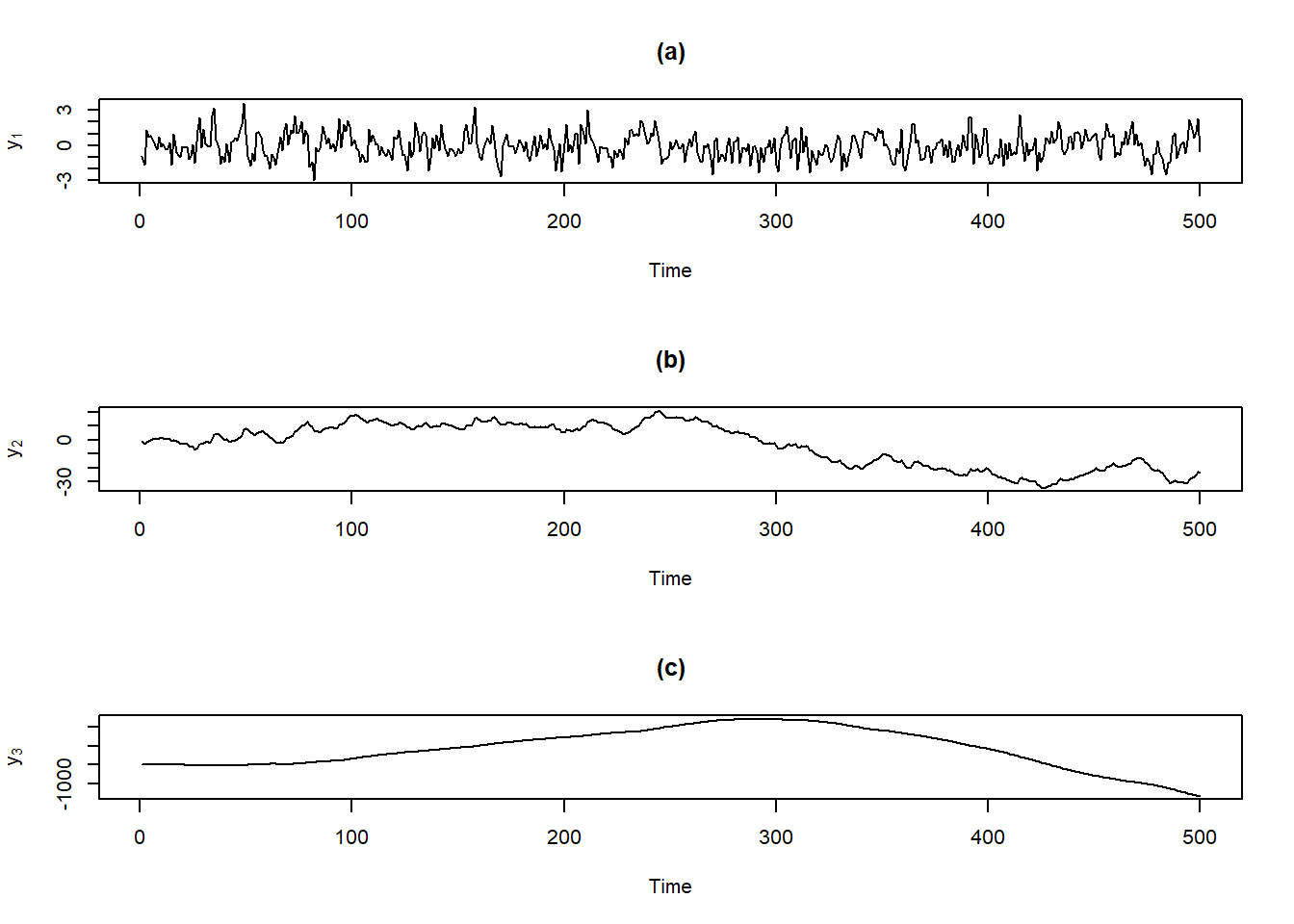
<- cumsum (y1) # cumsum : 누적합 <- cumsum (y2)par (mfrow= c (3 , 1 )) # 3개의 그래프를 한 화면에 출력 plot (y1, type = "l" , ylab = expression (y[1 ]),lwd = 1 , main = "(a)" )plot (y2, type = "l" ,xlab = "Time" , ylab = expression (y[2 ]),lwd = 1 , main = "(b)" )plot (y3, type = "l" ,xlab = "Time" , ylab = expression (y[3 ]),lwd = 1 , main = "(c)" )
Result! (a) 그래프는 평균 0 근처에서 무작위로 변하며, 정상시계열로 보인다.
CPI 데이터셋
CSV 파일에 저장되어 있는 CPI (계절 조정된 미국의 소비자 물가 지수) 데이터셋은 1913년 1월 31일부터 2001년 11월 30일까지 월별 CPI가 기록되어져 있다.
# 데이터 불러오기 <- read.csv (".../CPI.dat.csv" )head (CPI.dat)# 1977-01-31 ~ 1987-12-31 CPI만 추출 <- as.matrix (CPI.dat$ CPI)[769 : 900 ,] head (CPI)# log(CPI)를 차분 <- as.matrix (diff (log (CPI), diff = 1 )) # 1번 차분 head (CPI_diff1)<- as.matrix (diff (log (CPI), diff = 2 )) # 2번 차분 head (CPI_diff2)
X.Y..m..d CPI
1 1913-01-31 9.8
2 1913-02-28 9.8
3 1913-03-31 9.8
4 1913-04-30 9.8
5 1913-05-31 9.7
6 1913-06-30 9.8
[1] 58.7 59.3 59.6 60.0 60.2 60.5
[,1]
[1,] 0.010169579
[2,] 0.005046268
[3,] 0.006688988
[4,] 0.003327790
[5,] 0.004971013
[6,] 0.004946424
[,1]
[1,] -5.123311e-03
[2,] 1.642720e-03
[3,] -3.361198e-03
[4,] 1.643223e-03
[5,] -2.458879e-05
[6,] -2.434673e-05
Caution! 함수 diff()를 이용하여 시계열을 차분할 수 있으며, 옵션 diff에 차분 횟수를 입력하면 된다.
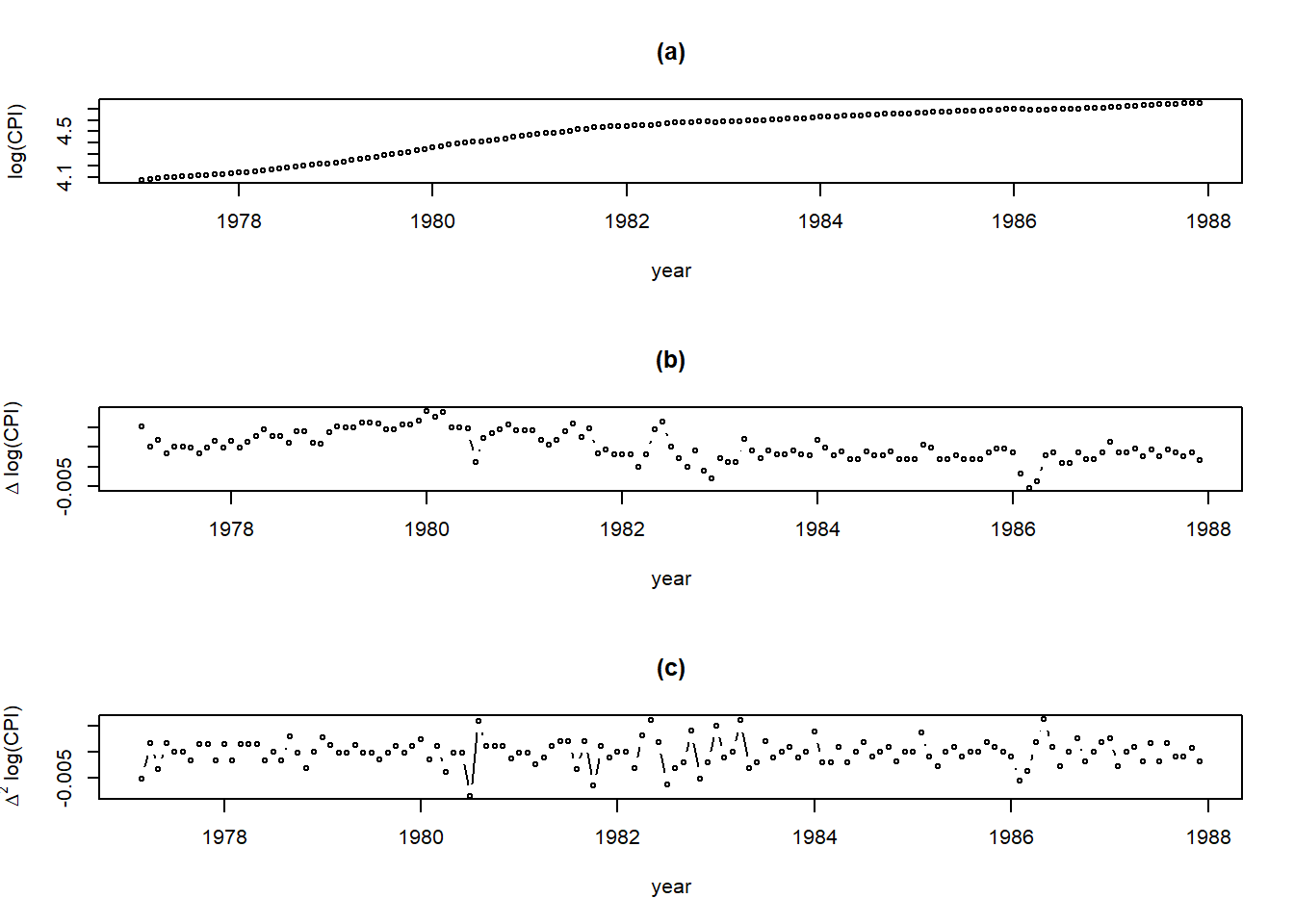
par (mfrow= c (3 , 1 )) # 3개의 그래프를 한 화면에 출력 plot (ts (log (CPI), # log(CPI)를 ts로 변환 start = c (1977 , 1 ), # 시계열의 시작 날짜 / c(1977, 1) : 1977년 1월 frequency = 12 ), # 주기 / 12 : 월별 시계열로 1년에 12번 관측 xlab = "year" , ylab = "log(CPI)" , # 축 이름 type = "b" , # 점과 선을 함께 표시 main = "(a)" ) # 제목 plot (ts (as.vector (CPI_diff1), # log(CPI)를 1번 차분한 시계열을 ts로 변환 start = c (1977 , 2 ), # 시계열의 시작 날짜 / c(1977, 2) : 1977년 2월 frequency = 12 ), xlab = "year" , ylab = expression (paste (Delta," log(CPI)" )),type = "b" ,main = "(b)" )plot (ts (as.vector (CPI_diff2), # log(CPI)를 2번 차분한 시계열을 ts로 변환 start = c (1977 , 3 ), # 시계열의 시작 날짜 / c(1977, 3) : 1977년 3월 frequency = 12 ), xlab = "year" , ylab = expression (paste (Delta^ 2 ," log(CPI)" )), type = "b" , main = "(c)" )
Caution! 함수 ts()를 이용하여 시계열 객체로 변환할 수 있으며, 옵션 start에는 시계열의 시작 날짜, 옵션 frequency에는 주기를 입력한다.Result! (a) 그래프를 통해 원 시계열 log(CPI)는 Momentum 현상을 보인다는 것을 알 수 있다.
ARIMA 모형
# 2번 차분한 log(CPI)에 MA(2) 모형 구축 <- arima (CPI_diff2,order = c (0 , 0 , 2 )) # (p, d, q)
Call:
arima(x = CPI_diff2, order = c(0, 0, 2))
Coefficients:
ma1 ma2 intercept
-0.3433 -0.3694 0e+00
s.e. 0.0831 0.0837 1e-04
sigma^2 estimated as 5.062e-06: log likelihood = 607.81, aic = -1207.62
Result! 2번 차분한 log(CPI)에 대해 구축된 MA(2) 모형, 즉, 원 시계열 log(CPI)에 대해 구축된 ARIMA(0,2,2) 모형은 \((1-B)^2Y_t=\epsilon_t-0.3433\epsilon_{t-1}-0.3694\epsilon_{t-2}\) 이다.
# 잔차를 이용한 모형 진단 Box.test (fit_ma$ resid, # 잔차 lag = 20 , type = "Ljung-Box" ,fitdf = 2 ) # 추정된 theta 개수
Box-Ljung test
data: fit_ma$resid
X-squared = 26.956, df = 18, p-value = 0.07983
Result! 귀무가설 \(H_0 : \rho(1)=\rho(2)=\cdots=\rho(20)=0\) 에 대한 검정 결과에 따르면, \(p\) 값이 0.07983이므로 유의수준 0.05에서 \(p\) 값이 0.05보다 크기 때문에 귀무가설을 기각하지 못한다. 즉, 잔차에 대해 시차 20까지의 자기상관계수 \(\rho(1), \rho(2), \cdots, \rho(20)\) 중 유의한 자기상관계수가 적어도 1개 존재한다는 증거가 부족하며, 2번 차분한 log(CPI)에 대해 MA(2) 모형을 가정하는 것이 적절하다.
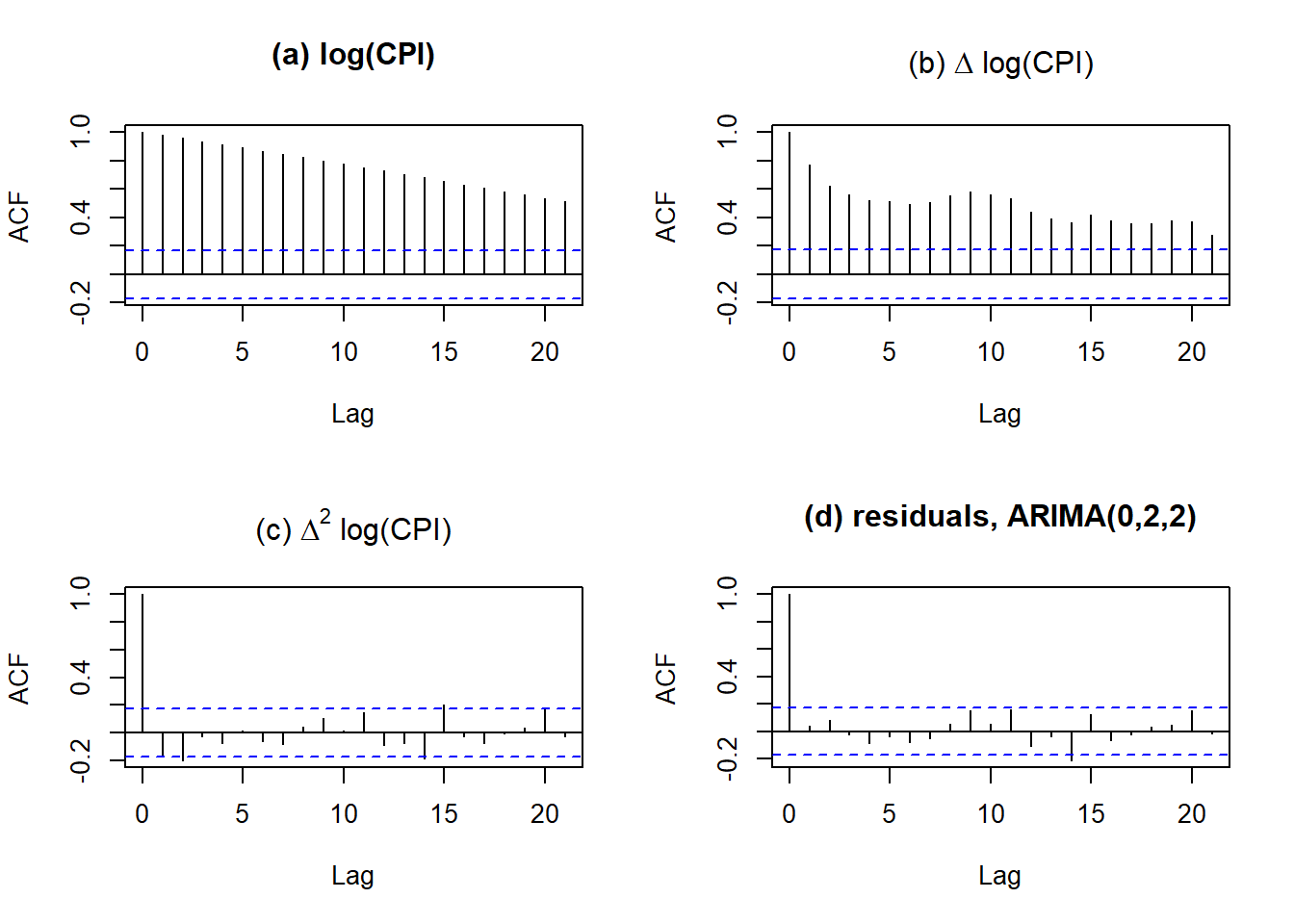
par (mfrow= c (2 ,2 )) # 1행에 2개의 그래프를 출력 -> 총 2개의 행으로 4개의 그래프가 출력됨 acf (log (CPI),main = "(a) log(CPI)" )acf (CPI_diff1, main = expression (paste ("(b) " ,Delta," log(CPI)" )))acf (CPI_diff2, main = expression (paste ("(c) " ,Delta^ 2 ," log(CPI)" )))acf (fit_ma$ resid, main = "(d) residuals, ARIMA(0,2,2)" )
Result! (a) 그래프를 통해 원 시계열 log(CPI)의 자기상관계수 ACF는 천천히 감소하고 있다는 것을 알 수 있으며, 이는 원 시계열이 비정상시계열임을 의미한다.
Mishkin 데이터셋
Package "Ecdat"에서 제공하는 Mishkin 데이터셋은 1950년 2월부터 1990년 12월 사이에 인플레이션율에 대한 시계열 데이터셋이다.
# 패키지 설치 :: p_load ("Ecdat" )# 데이터 불러오기 data (Mishkin, package = "Ecdat" )<- as.vector (Mishkin[,1 ]) # 월별 인플레이션율 추출
[1] -3.552289 5.247540 1.692860 5.064298 6.719322 11.668920 9.912501 8.346786 6.517766 4.865085 16.076321 19.154240 14.061910 4.650814 1.546310 4.627010 -1.540355 1.540355 0.000000
[20] 7.672257 6.102576 6.209472 4.533152 0.000000 -7.564866 0.000000 19.570490 -1.494151 1.494151 0.000000 -1.494151 0.000000 1.494151 0.000000 -1.494151 -2.993894 -6.010291 3.008908
[39] 1.501630 2.997634 4.482457 2.979029 2.971549 1.483071 2.960655 -4.443726 -1.484906 2.967978 -1.483071 -1.484906 -2.839906 2.839906 1.484906 0.000000 -1.484906 -2.839906 -2.982291
[58] 2.982291 -2.982291 0.000000 0.000000 1.492020 0.000000 0.000000 0.000000 2.978693 -2.978693 4.330177 0.000000 1.484906 -2.836390 0.000000 0.000000 2.836390 1.483071 5.914023
[77] 5.751562 8.774637 -1.457907 1.457907 5.682521 1.449363 2.893485 0.000000 2.886525 2.748830 2.873018 2.866156 7.006195 5.678584 1.415482 1.413814 0.000000 4.103441 0.000000
[96] 7.020216 1.399128 6.844860 2.777502 0.000000 1.386248 1.384744 0.000000 0.000000 1.383148 1.381556 -1.381556 1.381556 -1.381556 0.000000 1.381556 1.254555 5.504627 2.742874
[115] -1.370653 2.739743 3.973921 1.363010 -2.727571 1.364560 0.000000 6.799529 0.000000 2.586158 0.000000 0.000000 1.352397 5.394306 1.344819 0.000000 0.000000 1.343314 -1.343314
[134] 1.343314 0.000000 1.341812 5.230890 -1.335972 2.670459 0.000000 0.000000 0.000000 0.000000 2.664529 2.658626 2.532271 0.000000 0.000000 2.647071 0.000000 6.592472 -1.315600
[153] 0.000000 -1.317044 1.317044 1.315600 1.194725 0.000000 0.000000 5.242814 3.917133 0.000000 1.302875 1.183181 0.000000 2.598952 0.000000 0.000000 -1.298772 1.298772 2.593336
[172] 0.000000 2.587653 1.291782 -1.291782 2.582175 1.171857 2.574118 1.284992 -1.284992 0.000000 1.284992 3.846739 2.557659 6.254851 1.270154 -2.541654 2.541654 0.000000 2.536194
[191] 3.679570 0.000000 7.553715 2.393494 4.999561 0.000000 2.491991 2.486741 7.317456 1.233940 4.811423 0.000000 0.000000 0.000000 1.227743 2.451723 2.446724 3.549967 3.649961
[210] 4.849325 2.307577 3.617287 3.606416 2.289339 3.588767 4.768305 3.456034 4.735883 3.539687 4.596686 3.515803 3.399432 3.495549 3.485477 5.681739 3.458990 2.300467 3.338259
[229] 4.574945 6.726781 5.662605 3.282331 7.861482 3.252032 4.457231 4.339972 4.424734 5.408054 7.570396 2.182552 5.439077 3.153226 7.553640 4.197689 3.211568 5.236804 2.126986
[248] 4.242622 6.240278 4.110415 5.237093 2.088382 5.110830 5.183215 6.096802 5.041712 6.133401 2.962434 1.016681 1.015820 2.029064 1.013247 3.952596 1.009064 5.945445 3.007194
[267] 2.999539 2.901685 2.984980 2.977574 2.880218 4.934430 2.950948 3.834231 2.934329 5.758887 8.630559 11.440700 9.436906 6.536329 7.438794 3.659775 19.304211 1.838323 7.242186
[286] 8.105994 8.051480 9.785962 15.814170 12.122030 6.883693 12.010690 10.111450 7.566704 13.394280 12.342670 9.006326 9.680984 7.246837 4.855838 6.371189 4.738003 4.719480 5.566699
[305] 9.340268 12.388900 4.665991 5.350513 6.864336 6.061113 5.269925 3.040442 3.720887 3.778037 5.200997 6.673568 7.379198 5.857414 5.093520 5.072093 5.117023 3.575525 5.014266
[324] 6.435108 12.054450 6.336976 9.123064 6.255971 7.616233 4.105433 4.782352 2.760079 4.065748 5.420399 4.033883 6.056223 7.374409 8.668254 9.873637 10.451070 11.012750 5.793180
[343] 5.119508 7.025764 7.623123 6.306279 6.273224 9.946648 11.106510 10.389710 11.519510 13.766670 11.877010 9.987637 9.318593 10.410780 9.167216 6.281625 9.620259 14.005740 14.956960
[362] 14.772750 8.707769 10.170030 8.572340 7.396264 9.999892 11.967070 7.265405 7.174647 7.693233 10.614180 15.060890 9.936591 6.880011 7.334265 6.843737 9.197388 8.644333 9.498251
[381] 5.220479 4.722268 4.229963 6.531282 3.765132 1.835451 1.875277 8.318006 11.909480 8.179443 2.243804 5.880264 5.358331 1.808168 0.903063 2.664138 0.409372 0.818200 8.558391
[400] 6.479959 4.032262 4.820824 4.002672 5.979086 3.176779 1.981179 1.582568 6.702875 5.491976 2.736532 5.843219 3.492417 3.868475 3.856044 4.994358 5.737063 3.048542 0.000000
[419] 0.760985 2.279948 4.924980 5.281344 4.883469 4.490115 3.729027 1.860177 2.599458 3.703707 3.692311 4.048485 2.935736 3.659655 -3.293165 -5.508809 -2.579503 3.683244 5.869799
[438] 0.365932 2.193139 5.828813 1.089709 1.088720 1.087844 7.226761 4.308729 5.364409 6.405601 4.251591 4.236581 3.167622 6.310269 6.277260 3.126359 1.040348 0.000000 3.115431
[457] 3.107574 5.161263 6.164397 4.092111 5.095515 5.073969 5.052708 8.040197 3.999936 0.998057 1.993322 5.960278 4.944349 6.888122 7.823956 6.804426 2.904398 2.897386 1.927679
[476] 3.846190 5.746220 2.862824 1.904730 12.307830 5.638225 6.544558 1.863323 2.789618 6.484031 4.610040 10.992540 9.988676 7.212614 2.693695 0.000000
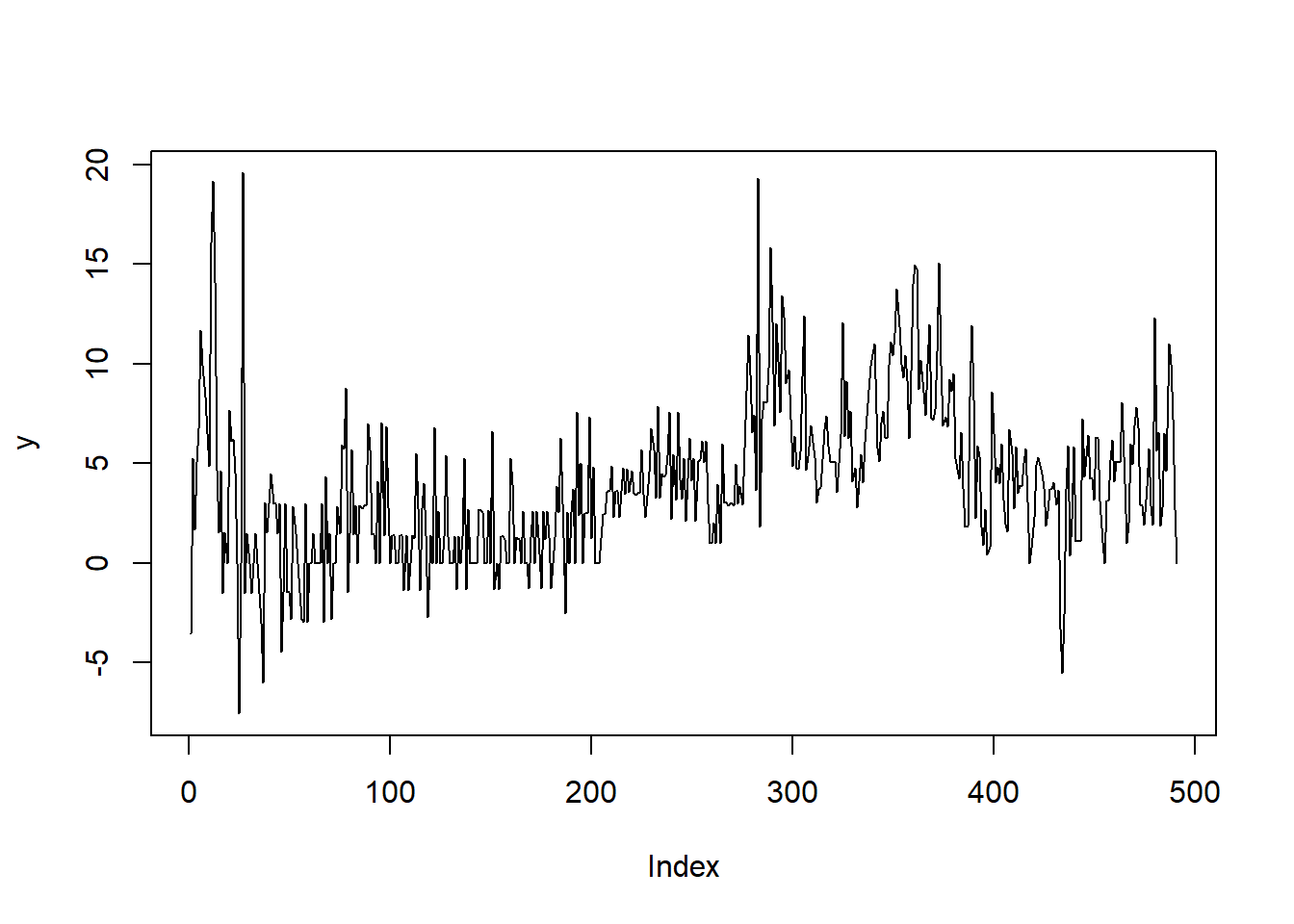
# 시계열 그림 plot (y, type = "l" )
Result! 시간의 흐름에 따라 평균이 변하므로 원 시계열은 비정상시계열임이 의심된다.
단위근 검정
# 패키지 설치 :: p_load ("tseries" )# Dickey-Fuller test adf.test (y)
Augmented Dickey-Fuller Test
data: y
Dickey-Fuller = -3.8651, Lag order = 7, p-value = 0.01576
alternative hypothesis: stationary
# Phillips-Perron test pp.test (y)
Phillips-Perron Unit Root Test
data: y
Dickey-Fuller Z(alpha) = -248.75, Truncation lag parameter = 5, p-value = 0.01
alternative hypothesis: stationary
KPSS Test for Level Stationarity
data: y
KPSS Level = 2.51, Truncation lag parameter = 5, p-value = 0.01
Caution! 단위근 검정을 수행하기 위해 Package "tseries"에서 제공하는 함수 adf.test(), pp.test(), kpss.test()를 사용한다.Result! 1. Dickey-Fuller test를 수행했을 때, \(p\) 값이 0.01576이므로 유의수준 0.05에서 \(p\) 값이 0.05보다 작기 때문에 귀무가설을 기각한다. 즉, 관측된 시계열은 정상성을 만족한다.\(p\) 값이 0.01이므로 유의수준 0.05에서 \(p\) 값이 0.05보다 작기 때문에 귀무가설을 기각한다. 즉, 관측된 시계열은 정상성을 만족한다.\(p\) 값이 0.01이므로 유의수준 0.05에서 \(p\) 값이 0.05보다 작기 때문에 귀무가설을 기각한다. 즉, 단위근이 존재하므로 관측된 시계열은 비정상성을 가진다.
ARIMA 모형
# 패키지 설치 :: p_load ("forecast" )auto.arima (y,max.p = 5 , max.q = 5 , ic = "bic" ) # BIC 기준으로 BIC가 가장 작은 모형을 최적 모형으로 선택
Series: y
ARIMA(1,1,1)
Coefficients:
ar1 ma1
0.2383 -0.8772
s.e. 0.0550 0.0269
sigma^2 = 8.587: log likelihood = -1221.62
AIC=2449.25 AICc=2449.29 BIC=2461.83
# ARIMA(1,1,1) 모형 구축 <- arima (y, c (1 , 1 , 1 ))
Result! 함수 auto.arima()를 이용하여 BIC 기준으로 최적의 모형을 판단했을 때, ARIMA(1,1,1) 모형이 선택되었다. 추정된 모수 결과를 이용하면 구축된 ARIMA(1,1,1) 모형은 \((1-B)Y_t = 0.2383Y_{t-1}+\epsilon_t -0.8772\epsilon_{t-1}\) 이다.
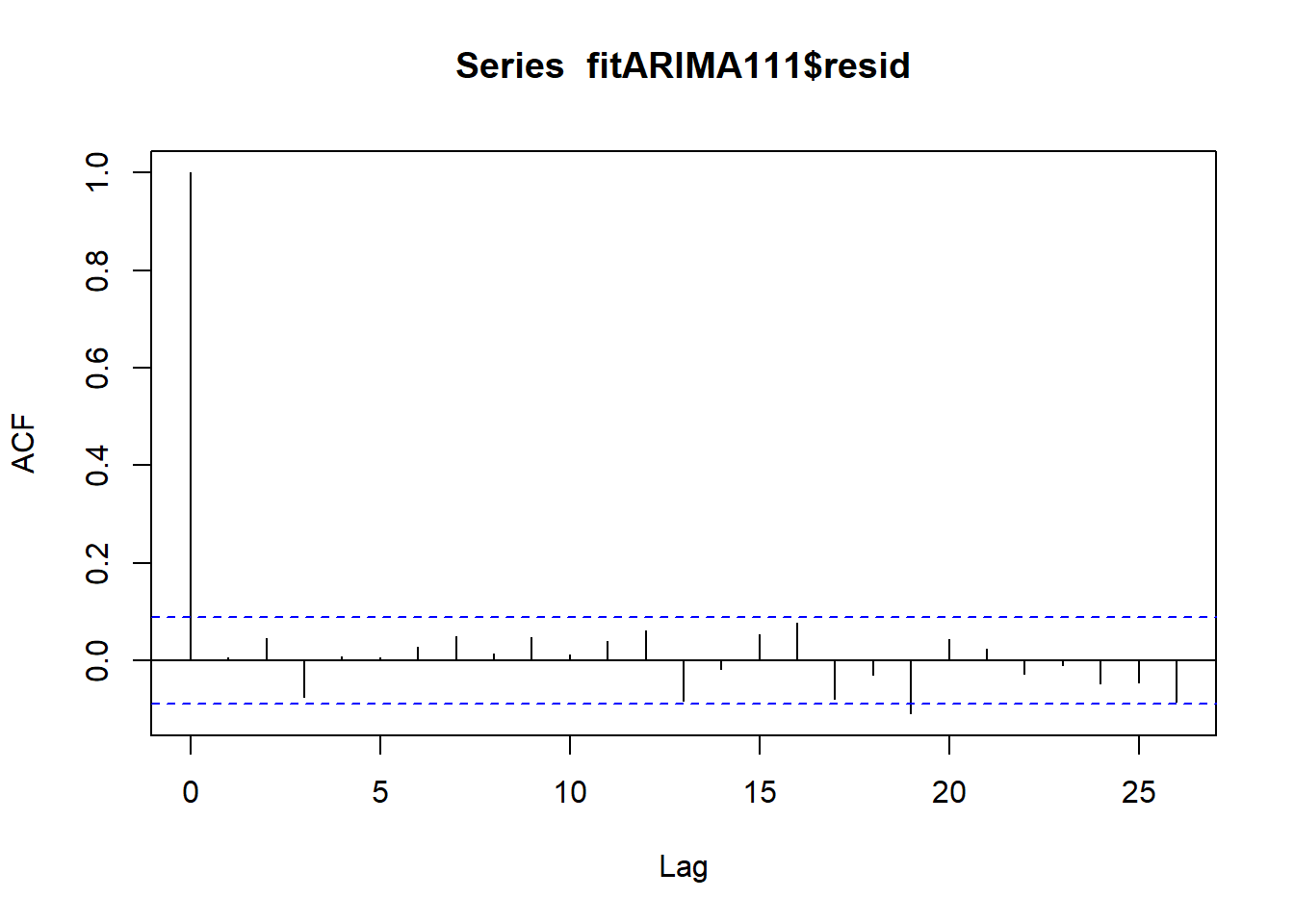
# 잔차를 이용한 모형 진단 par (mfrow= c (1 ,1 ))acf (fitARIMA111$ resid) Box.test (fitARIMA111$ resid,lag = 15 ,fitdf = 2 ) # 추정한 phi와 theta 개수
Box-Pierce test
data: fitARIMA111$resid
X-squared = 14.442, df = 13, p-value = 0.3435
Result! 잔차의 자기상관계수 ACF 그래프를 보면 시차 0을 제외하고 막대의 끝이 파란색 선을 넘어가지 않으므로 다른 시차에서 자기상관계수가 통계적으로 유의하다는 증거가 부족하다.\(H_0 : \rho(1)=\rho(2)=\cdots=\rho(15)=0\) 에 대해 \(p\) 값이 0.3435이므로 유의수준 0.05에서 \(p\) 값이 0.05보다 크기 때문에 귀무가설을 기각하지 못한다. 즉, 잔차에 대해 시차 15까지의 자기상관계수 \(\rho(1), \rho(2), \cdots, \rho(15)\) 중 유의한 자기상관계수가 적어도 1개 존재한다는 증거가 부족하며, 해당 시계열에 대해 ARIMA(1,1,1) 모형을 가정하는 것이 적절하다.
예측
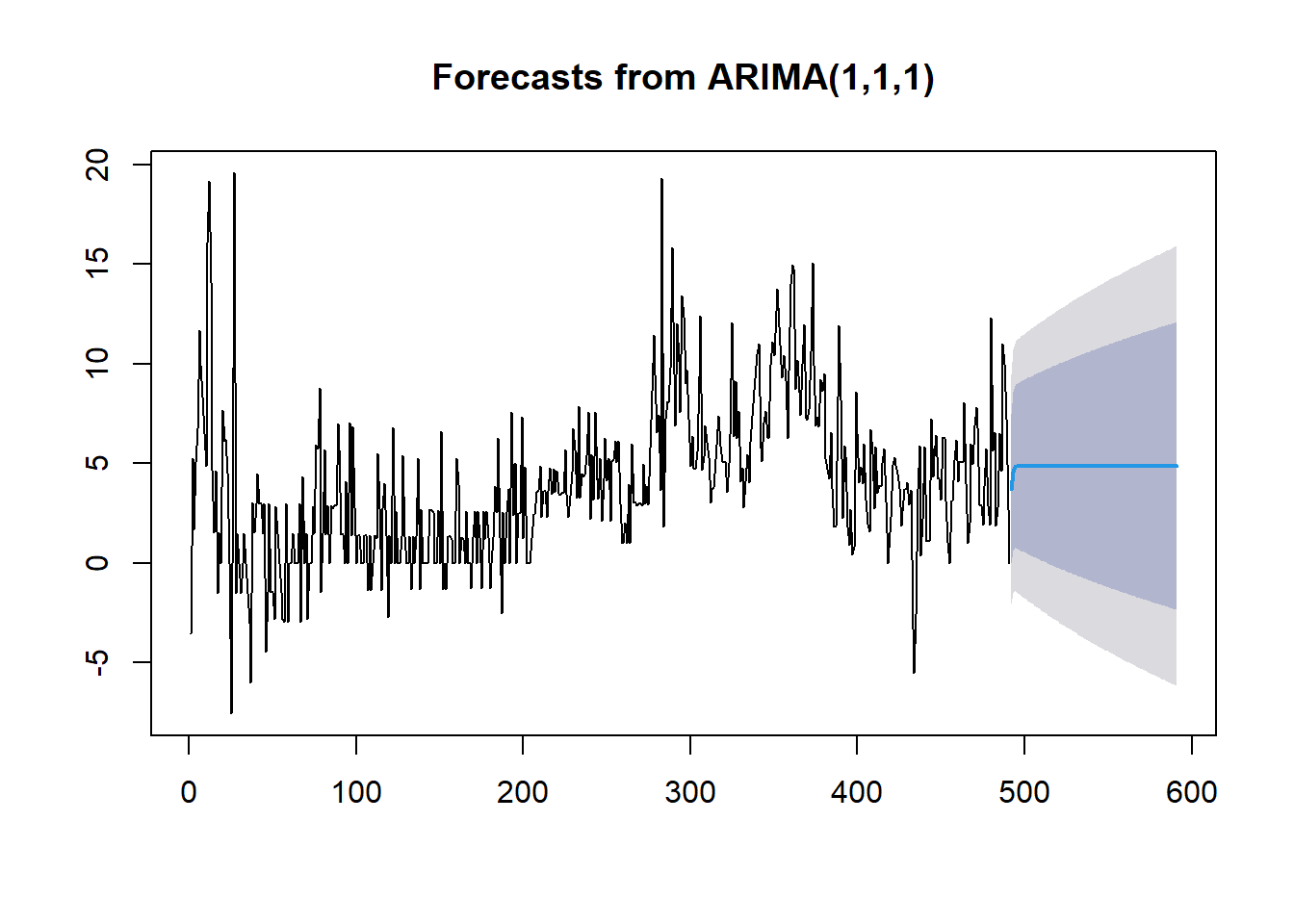
<- forecast (fitARIMA111,h = 100 ) # 미래 100시점까지 예측
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
492 3.706101 -0.04167452 7.453876 -2.025627 9.437828
493 4.589298 0.60462429 8.573972 -1.504735 10.683331
494 4.799773 0.73892466 8.860620 -1.410758 11.010303
495 4.849930 0.73788314 8.961978 -1.438903 11.138764
496 4.861884 0.70417897 9.019588 -1.496777 11.220544
497 4.864732 0.66298827 9.066476 -1.561281 11.290745
498 4.865411 0.62034731 9.110475 -1.626854 11.357676
499 4.865573 0.57768877 9.153457 -1.692180 11.423325
500 4.865611 0.53534501 9.195878 -1.756959 11.488182
501 4.865620 0.49338614 9.237855 -1.821135 11.552376
502 4.865623 0.45182011 9.279425 -1.884706 11.615951
503 4.865623 0.41064046 9.320606 -1.947685 11.678931
504 4.865623 0.36983763 9.361409 -2.010088 11.741334
505 4.865623 0.32940172 9.401845 -2.071929 11.803176
506 4.865623 0.28932308 9.441924 -2.133224 11.864471
507 4.865623 0.24959239 9.481654 -2.193987 11.925233
508 4.865623 0.21020076 9.521046 -2.254231 11.985478
509 4.865623 0.17113966 9.560107 -2.313970 12.045217
510 4.865623 0.13240091 9.598846 -2.373216 12.104462
511 4.865623 0.09397664 9.637270 -2.431981 12.163227
512 4.865623 0.05585933 9.675387 -2.490276 12.221523
513 4.865623 0.01804173 9.713205 -2.548113 12.279360
514 4.865623 -0.01948312 9.750730 -2.605502 12.336749
515 4.865623 -0.05672191 9.787969 -2.662454 12.393701
516 4.865623 -0.09368109 9.824928 -2.718978 12.450225
517 4.865623 -0.13036685 9.861614 -2.775084 12.506331
518 4.865623 -0.16678519 9.898032 -2.830781 12.562028
519 4.865623 -0.20294187 9.934189 -2.886078 12.617325
520 4.865623 -0.23884244 9.970089 -2.940983 12.672230
521 4.865623 -0.27449228 10.005739 -2.995505 12.726752
522 4.865623 -0.30989655 10.041143 -3.049651 12.780898
523 4.865623 -0.34506028 10.076307 -3.103430 12.834676
524 4.865623 -0.37998830 10.111235 -3.156847 12.888094
525 4.865623 -0.41468527 10.145932 -3.209912 12.941158
526 4.865623 -0.44915574 10.180402 -3.262630 12.993876
527 4.865623 -0.48340408 10.214651 -3.315008 13.046255
528 4.865623 -0.51743452 10.248681 -3.367053 13.098300
529 4.865623 -0.55125118 10.282498 -3.418771 13.150018
530 4.865623 -0.58485803 10.316105 -3.470169 13.201415
531 4.865623 -0.61825894 10.349506 -3.521251 13.252498
532 4.865623 -0.65145763 10.382704 -3.572024 13.303271
533 4.865623 -0.68445775 10.415704 -3.622493 13.353740
534 4.865623 -0.71726281 10.448509 -3.672664 13.403911
535 4.865623 -0.74987622 10.481123 -3.722542 13.453789
536 4.865623 -0.78230132 10.513548 -3.772132 13.503379
537 4.865623 -0.81454132 10.545788 -3.821439 13.552686
538 4.865623 -0.84659937 10.577846 -3.870467 13.601714
539 4.865623 -0.87847849 10.609725 -3.919222 13.650469
540 4.865623 -0.91018167 10.641428 -3.967708 13.698955
541 4.865623 -0.94171177 10.672958 -4.015929 13.747176
542 4.865623 -0.97307161 10.704318 -4.063890 13.795137
543 4.865623 -1.00426392 10.735511 -4.111595 13.842841
544 4.865623 -1.03529134 10.766538 -4.159047 13.890294
545 4.865623 -1.06615646 10.797403 -4.206251 13.937498
546 4.865623 -1.09686182 10.828108 -4.253211 13.984457
547 4.865623 -1.12740986 10.858657 -4.299930 14.031177
548 4.865623 -1.15780297 10.889050 -4.346412 14.077659
549 4.865623 -1.18804350 10.919290 -4.392661 14.123908
550 4.865623 -1.21813371 10.949380 -4.438680 14.169927
551 4.865623 -1.24807582 10.979322 -4.484473 14.215719
552 4.865623 -1.27787201 11.009119 -4.530042 14.261289
553 4.865623 -1.30752437 11.038771 -4.575391 14.306638
554 4.865623 -1.33703499 11.068282 -4.620524 14.351771
555 4.865623 -1.36640586 11.097653 -4.665443 14.396689
556 4.865623 -1.39563896 11.126886 -4.710151 14.441398
557 4.865623 -1.42473620 11.155983 -4.754651 14.485898
558 4.865623 -1.45369947 11.184946 -4.798947 14.530194
559 4.865623 -1.48253060 11.213777 -4.843040 14.574287
560 4.865623 -1.51123138 11.242478 -4.886934 14.618181
561 4.865623 -1.53980356 11.271050 -4.930632 14.661878
562 4.865623 -1.56824885 11.299496 -4.974135 14.705382
563 4.865623 -1.59656893 11.327816 -5.017447 14.748694
564 4.865623 -1.62476545 11.356012 -5.060570 14.791816
565 4.865623 -1.65283999 11.384087 -5.103506 14.834753
566 4.865623 -1.68079414 11.412041 -5.146258 14.877505
567 4.865623 -1.70862943 11.439876 -5.188829 14.920075
568 4.865623 -1.73634736 11.467594 -5.231220 14.962466
569 4.865623 -1.76394940 11.495196 -5.273433 15.004680
570 4.865623 -1.79143700 11.522684 -5.315472 15.046719
571 4.865623 -1.81881157 11.550058 -5.357338 15.088584
572 4.865623 -1.84607448 11.577321 -5.399033 15.130279
573 4.865623 -1.87322710 11.604474 -5.440559 15.171806
574 4.865623 -1.90027075 11.631517 -5.481919 15.213165
575 4.865623 -1.92720674 11.658453 -5.523114 15.254360
576 4.865623 -1.95403634 11.685283 -5.564146 15.295393
577 4.865623 -1.98076080 11.712007 -5.605018 15.336264
578 4.865623 -2.00738135 11.738628 -5.645730 15.376977
579 4.865623 -2.03389918 11.765146 -5.686286 15.417532
580 4.865623 -2.06031549 11.791562 -5.726686 15.457933
581 4.865623 -2.08663142 11.817878 -5.766933 15.498179
582 4.865623 -2.11284812 11.844095 -5.807028 15.538274
583 4.865623 -2.13896670 11.870213 -5.846973 15.578219
584 4.865623 -2.16498824 11.896235 -5.886769 15.618016
585 4.865623 -2.19091383 11.922160 -5.926419 15.657666
586 4.865623 -2.21674452 11.947991 -5.965924 15.697170
587 4.865623 -2.24248134 11.973728 -6.005285 15.736531
588 4.865623 -2.26812530 11.999372 -6.044504 15.775750
589 4.865623 -2.29367742 12.024924 -6.083582 15.814829
590 4.865623 -2.31913866 12.050385 -6.122522 15.853769
591 4.865623 -2.34450999 12.075757 -6.161324 15.892571
Caution! 예측은 Package "forecast"에서 제공하는 함수 forecast()를 이용하여 수행할 수 있다.
Result! 원 시계열은 비정상성을 가지기 때문에 예측 구간은 발산한다는 것을 알 수 있다.
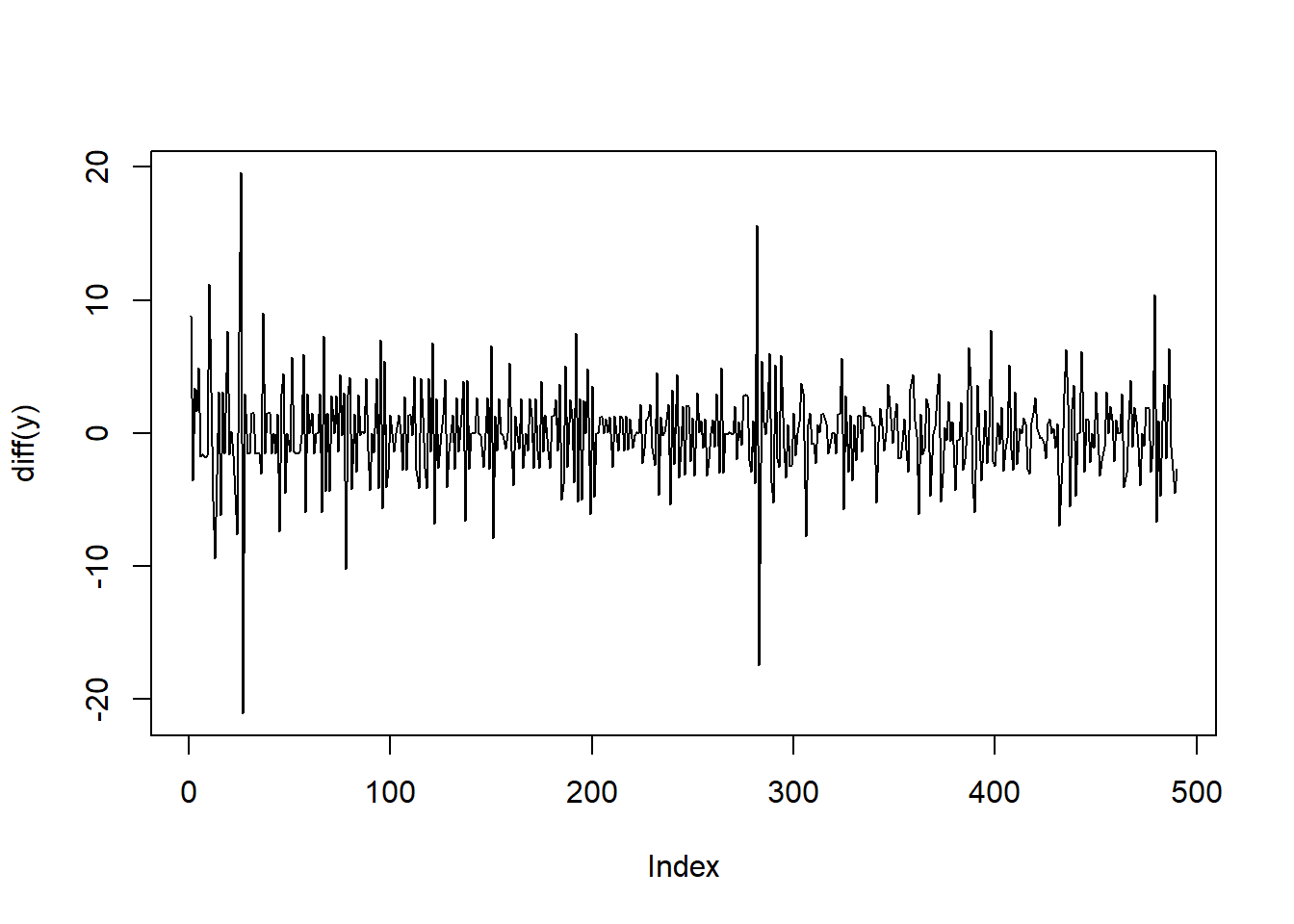
# 1번 차분한 시계열에 대한 예측 ## 시계열 그림 plot (diff (y), type = "l" )
Result! 1번 차분한 시계열은 시간의 흐름에 따라 평균이 변하지 않고 분산도 일정해 보이므로 정상시계열로 보인다.
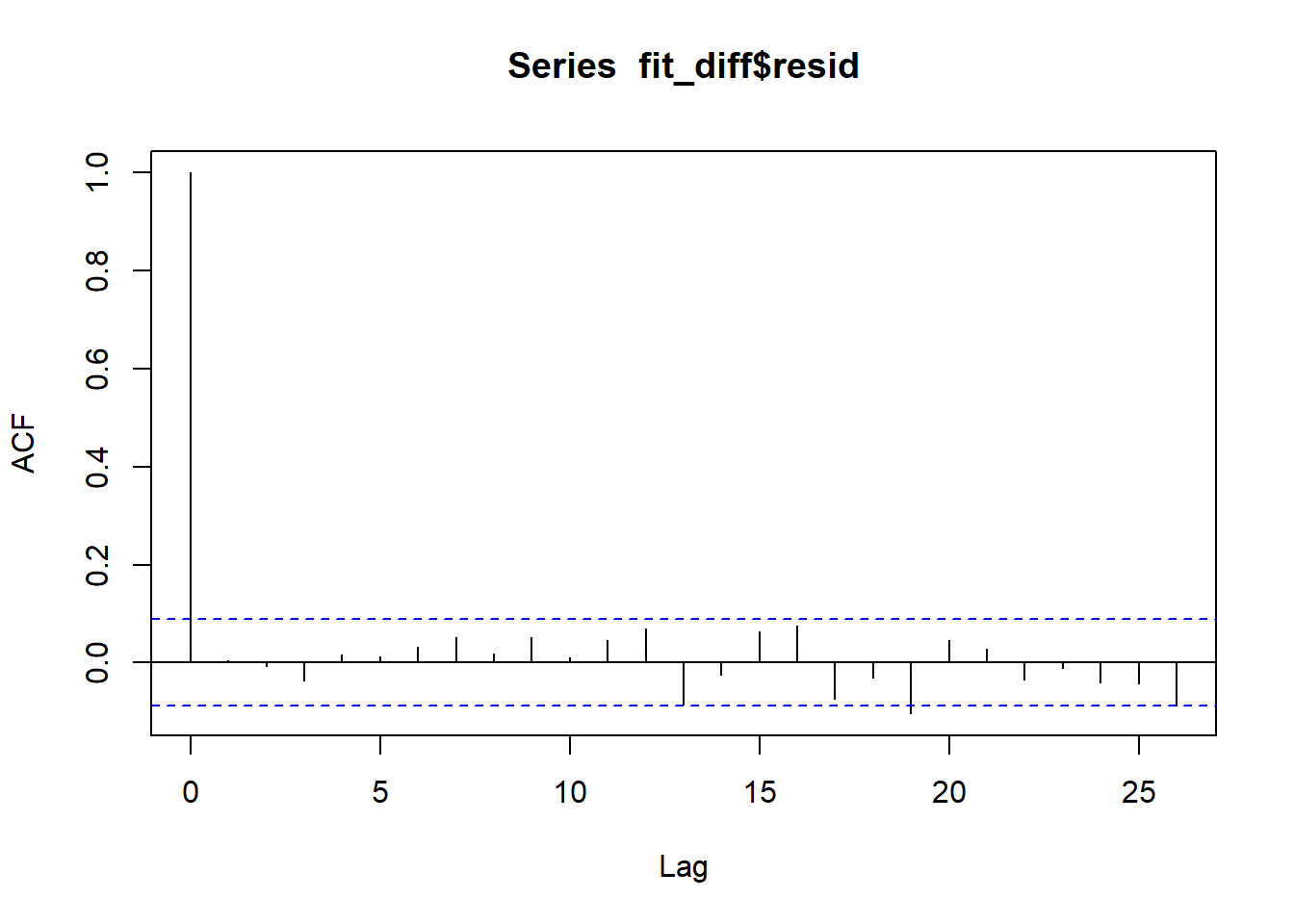
# 1번 차분한 시계열에 MA(3) 모형 구축 <- arima (diff (y),order = c (0 , 0 , 3 ))# 잔차를 이용한 모형 진단 acf (fit_diff$ resid) Box.test (fit_diff$ resid,lag = 15 ,fitdf = 3 )
Box-Pierce test
data: fit_diff$resid
X-squared = 13.346, df = 12, p-value = 0.3444
Result! 잔차의 자기상관계수 ACF 그래프를 보면 시차 0을 제외하고 막대의 끝이 파란색 선을 넘어가지 않으므로 다른 시차에서 자기상관계수가 통계적으로 유의하다는 증거가 부족하다.\(H_0 : \rho(1)=\rho(2)=\cdots=\rho(15)=0\) 에 대해 \(p\) 값이 0.3444이므로 유의수준 0.05에서 \(p\) 값이 0.05보다 크기 때문에 귀무가설을 기각하지 못한다. 즉, 잔차에 대해 시차 15까지의 자기상관계수 \(\rho(1), \rho(2), \cdots, \rho(15)\) 중 유의한 자기상관계수가 적어도 1개 존재한다는 증거가 부족하며, 해당 시계열에 대해 MA(3) 모형을 가정하는 것이 적절하다. 이는 1번 차분한 시계열은 정상시계열임을 의미한다.
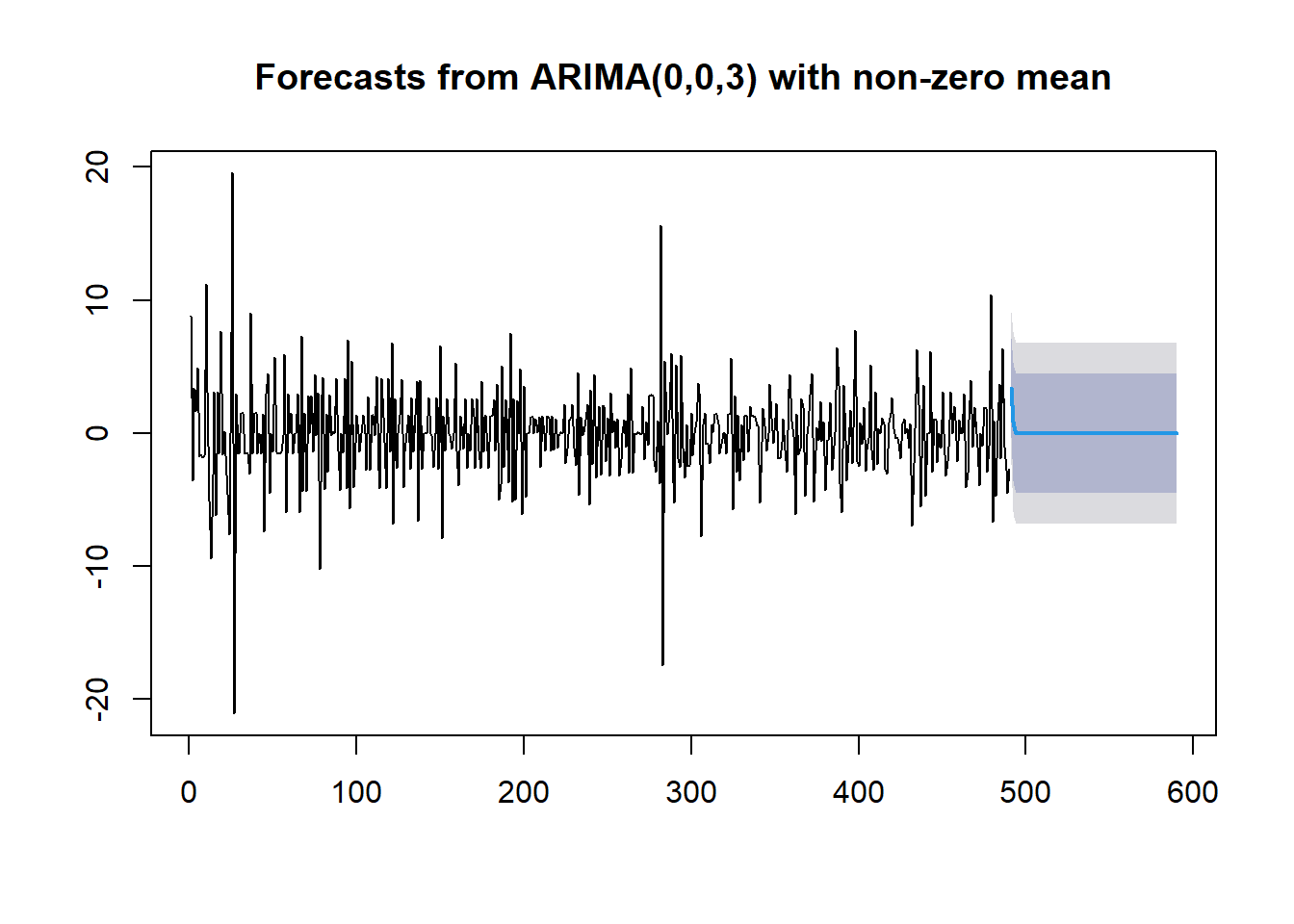
# 예측 <- forecast (fit_diff,h = 100 ) # 미래 100시점까지 예측
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
491 3.4279770957 -0.3093655 7.165320 -2.287795 9.143749
492 0.8929253001 -3.5301468 5.315997 -5.871580 7.657430
493 0.5146289502 -3.9250766 4.954335 -6.275315 7.304573
494 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
495 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
496 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
497 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
498 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
499 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
500 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
501 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
502 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
503 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
504 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
505 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
506 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
507 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
508 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
509 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
510 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
511 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
512 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
513 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
514 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
515 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
516 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
517 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
518 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
519 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
520 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
521 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
522 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
523 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
524 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
525 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
526 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
527 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
528 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
529 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
530 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
531 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
532 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
533 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
534 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
535 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
536 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
537 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
538 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
539 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
540 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
541 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
542 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
543 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
544 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
545 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
546 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
547 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
548 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
549 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
550 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
551 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
552 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
553 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
554 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
555 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
556 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
557 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
558 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
559 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
560 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
561 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
562 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
563 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
564 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
565 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
566 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
567 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
568 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
569 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
570 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
571 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
572 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
573 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
574 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
575 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
576 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
577 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
578 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
579 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
580 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
581 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
582 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
583 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
584 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
585 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
586 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
587 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
588 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
589 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
590 -0.0001564659 -4.4582307 4.457918 -6.818193 6.817880
Result! 원 시계열을 1번 차분한 시계열은 정상성을 가지기 때문에 예측 구간은 수렴한다는 것을 알 수 있다.