Dataset : Ridership on Amtrak Trains(미국 철도 회사 “Amtrak”에서 수집한 1991년 1월~2004년 3월까지 매달 환승 고객 수)
Data Loading
:: p_load ("doParallel" , "parallel" ,"data.table" , "readr" ,"skimr" , "summarytools" , "DT" ,"dplyr" , "magrittr" ,"ggplot2" ,"caret" , "recipes" ,"keras" , # keras's Ver. 2.9.0 "tfdatasets" ) # For as_array_iterator registerDoParallel (cores= detectCores ()):: as_tensor (1 ) # systemMemory and maxCacheSize
tf.Tensor(1.0, shape=(), dtype=float64)
# Loading as Tibble Type <- readr:: read_csv (".../Amtrak.csv" ) %>%
# A tibble: 159 × 2
Month Ridership
<chr> <dbl>
1 01/01/1991 1709.
2 01/02/1991 1621.
3 01/03/1991 1973.
4 01/04/1991 1812.
5 01/05/1991 1975.
6 01/06/1991 1862.
7 01/07/1991 1940.
8 01/08/1991 2013.
9 01/09/1991 1596.
10 01/10/1991 1725.
# ℹ 149 more rows
코드 설명 함수 readr::read_csv()는 CSV 파일을 tibble 형태로 읽어온다. 이는 데이터 가독성과 처리 속도를 높이며, Package "tidyverse"와의 호환성을 향상시킨다.
Data Partition
<- round (nrow (Amtrak.data1) * 0.55 ) <- round (nrow (Amtrak.data1) * 0.25 ) <- nrow (Amtrak.data1) - num_train_samples - num_val_samples <- Amtrak.data1[seq (num_train_samples), ] # First 55% of Rows, 1:87 <- Amtrak.data1[seq (from = nrow (train_df) + 1 , # Next 25% of Rows, 88:127 length.out = num_val_samples), ] <- Amtrak.data1[seq (to = nrow (Amtrak.data1), # Last 20% of Rows, 128:159 length.out = num_test_samples), ]
# Training Dataset (TrD) :: datatable (train_df)
# Validation Dataset (VaD) :: datatable (val_df)
# Test Dataset (TeD) :: datatable (test_df)
Preprocess
Standardization
# 1. Standardization for Numeric Feature ## Name of Feature <- names (Amtrak.data1) %>% setdiff (c ("Date.Time" , "Ridership" )) # 사용하지 않는 변수 "Date.Time"와 Target Ridership 제거
[1] "Month_X1" "Month_X2" "Month_X3" "Month_X4" "Month_X5" "Month_X6" "Month_X7" "Month_X8" "Month_X9" "Month_X10" "Month_X11" "Month_X12"
Caution! 표준화는 수치형 Feature에 적용하며, 해당 데이터셋에서는 Feature로 고려하는 모든 변수(Month_X1, Month_X2, Month_X3, Month_X4, Month_X5, Month_X6, Month_X7, Month_X8, Month_X9, Month_X10, Month_X11, Month_X12)가 수치형이다.
## Standardization <- recipe (Ridership ~ ., data = train_df) %>% # Define Formula / Ridership: Target step_normalize (all_of (input_data_colnames)) %>% # Standardization for All Feature prep (training = train_df, retain = TRUE ) # Calculation for Standardization <- juice (data_recipe) # Standardized TrD <- bake (data_recipe, val_df) # Standardized VaD <- bake (data_recipe, test_df) # Standardized TeD
Caution! Training Dataset의 수치형 Feature에 대한 평균과 표준편차를 이용하여 Training Dataset, Validation Dataset, 그리고 Test Dataset에 표준화를 수행한다.
코드 설명
step_normalize(all_of(input_data_colnames))
Target Ridership을 제외한 모든 수치형 Feature에 대해 표준화를 수행한다.
표준화란 데이터를 평균 = 0, 표준편차 = 1에 맞도록 변환하는 과정이다.
# Standardized TrD :: datatable (standard_train_df)
# Standardized TrD :: datatable (standard_val_df)
# Standardized TrD :: datatable (standard_test_df)
Analysis
# #Feature <- length (input_data_colnames)# CallBack <- list (callback_early_stopping (monitor = "val_loss" , # Metric (Monitor for Validation) patience = 50 # 50번의 epochs 후에도 loss가 향상되지 않으면 stop! callback_model_checkpoint (filepath = "Amtrack.keras" , monitor = "val_loss" , # 저장 Metric (Monitor for Validation) save_best_only = TRUE # 가장 좋은 결과를 저장 callback_reduce_lr_on_plateau ( monitor = "val_loss" ,factor = 0.1 , # 학습률 감소하는 요인: New Learning Rate (LR) = LR * factor patience = 10 # monitor = "val_loss"가 10번의 epochs 동안 향상되지 않으면 콜백 실행
Model Definition
Deep Neural Network (DNN)
set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% layer_flatten () %>% # Convert to 1D vector layer_dense (units = 16 , activation = "relu" ) %>% layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_1 (InputLayer) [(None, 12, 12)] 0
flatten (Flatten) (None, 144) 0
dense_1 (Dense) (None, 16) 2320
dense (Dense) (None, 1) 17
========================================================================================================================================================================================================
Total params: 2337 (9.13 KB)
Trainable params: 2337 (9.13 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
layer_input(shape = c(sequence_length, ncol_input_data)): Input 정의
shape: Input의 크기를 정의한다.
sequence_length: 한 번의 입력에서 사용하는 시간 스텝의 수로 Amtrack Dataset에서는 12이다.ncol_input_data: 각 시점의 Feature 개수이다.예를 들어, 입력 데이터가 (10, 3)의 형태라면, 10개의 시간 단계와 3개의 Feature를 포함한다.
Caution! layer_input(shape = c(sequence_length, 1))은 Feature가 없을 때, 그리고 Feature가 1개 있을 때 두 경우에 모두 사용된다. layer_flatten(): 1차원 벡터로 변환
예를 들어, (sequence_length, ncol_input_data) 크기의 Input은 sequence_length * ncol_input_data 크기의 1차원 벡터로 변환된다.
layer_dense(units = 16, activation = "relu"): Dense 계층
은닉층으로 16개의 뉴런을 포함한다.
활성화 함수로 ReLU(Rectified Linear Unit)를 사용한다.
layer_dense(units = 1)
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
model <- keras_model(inputs, outputs): 입력과 출력을 연결하여 딥러닝 모형 정의
Convolutional Neural Network 1D (CNN 1D)
set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% layer_conv_1d (filters = 8 , kernel_size = 6 , activation = "relu" ) %>% # kernel_size=Window Length, 6개월 단위의 변화나 트렌드에 초점 layer_max_pooling_1d (pool_size = 2 ) %>% # Down-Sampling = Reduce Size layer_conv_1d (filters = 8 , kernel_size = 3 , activation = "relu" ) %>% # Due to layer_max_pooling_1d(), kernel_size = 3 layer_global_average_pooling_1d () %>% # Average for Each Convolution Feature Map layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_1"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_2 (InputLayer) [(None, 12, 12)] 0
conv1d_1 (Conv1D) (None, 7, 8) 584
max_pooling1d (MaxPooling1D) (None, 3, 8) 0
conv1d (Conv1D) (None, 1, 8) 200
global_average_pooling1d (GlobalAveragePooling1D) (None, 8) 0
dense_2 (Dense) (None, 1) 9
========================================================================================================================================================================================================
Total params: 793 (3.10 KB)
Trainable params: 793 (3.10 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
layer_conv_1d(filters = 8, kernel_size = 6, activation = "relu"): 1D 콘벌루션 계층
filters: 콘벌루션 필터 개수를 입력한다.kernel_size: 모형이 학습할 데이터 패턴의 시간적 범위(시계열 윈도우 크기)를 결정한다(커널 크기: \(1\times\) kernel_size).
Amtrack Dataset에서의 권장 설정:
작은 패턴 탐지: kernel_size = 2 ~ kernel_size = 4
2~4개월 단위의 국소적인(Local) 패턴을 학습하는 데 유용
중간 패턴 탐지: kernel_size = 6
전체 시퀀스 탐지: kernel_size = 12
전체 12개월 데이터를 한 번에 학습(권장되지는 않음, 과적합 위험)
kernel_size은 sequence_length보다 큰 값을 입력할 수 없다. activation: 활성화 함수를 입력한다. layer_max_pooling_1d(pool_size = 2): 1D Max Pooling 계층 → 시계열 데이터의 차원을 축소
pool_size(= Max Pooling Window Length)를 “2”로 지정한다.strides의 경우 옵션 pool_size에 입력한 값이 Default(여기서는 2)이다.두 옵션을 통해 해당 계층에서 입력 데이터의 차원을 절반으로 축소한다.
함수 layer_max_pooling_1d() 다음에 입력한 함수 layer_conv_1d()의 옵션 kernel_size는 절반으로 축소한 “3”으로 지정한다.
layer_global_average_pooling_1d(): 이전 콘벌루션 계층의 결과를 1차원으로 변환layer_dense(units = 1): Dense 계층
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
Long Short-Term Memory (LSTM)
# 1. Simple LSTM set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% layer_lstm (units = 16 ) %>% # units : Dimension of Output Space (Hidden State) (Ref. https://jiwonkoh.tistory.com/188) layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_2"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_3 (InputLayer) [(None, 12, 12)] 0
lstm (LSTM) (None, 16) 1856
dense_3 (Dense) (None, 1) 17
========================================================================================================================================================================================================
Total params: 1873 (7.32 KB)
Trainable params: 1873 (7.32 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
layer_lstm(units = 16): LSTM 계층
units: LSTM 계층이 출력하는 벡터의 차원을 지정한다.
units = 16은 해당 LSTM 계층은 16차원의 벡터를 출력한다는 의미이다.이는 LSTM의 은닉 상태와 셀 상태의 크기를 정의하며, units의 값은 LSTM 계층이 각 타임스텝에서 출력하는 벡터의 차원이 된다.
더 큰 units 값은 더 복잡한 패턴 학습이 가능하지만 계산 비용 증가한다.
layer_dense(units = 1): Dense 계층 → LSTM 계층의 출력(16차원 벡터)을 단일 값으로 변환
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
# 2. Simple LSTM based on recurrent_dropout set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% layer_lstm (units = 32 , recurrent_dropout = 0.25 ) %>% # recurrent_dropout : Dropout Rate of Recurrent Units layer_dropout (0.5 ) %>% # Dropout Layer after the LSTM for Regularizing Dense Layer layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_3"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_4 (InputLayer) [(None, 12, 12)] 0
lstm_1 (LSTM) (None, 32) 5760
dropout (Dropout) (None, 32) 0
dense_4 (Dense) (None, 1) 33
========================================================================================================================================================================================================
Total params: 5793 (22.63 KB)
Trainable params: 5793 (22.63 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
layer_lstm(units = 32, recurrent_dropout = 0.25): LSTM 계층
units = 32: LSTM 계층이 출력할 벡터 차원은 32이다.
LSTM이 학습하는 복잡한 패턴의 표현력을 조절한다.
값이 클수록 복잡한 패턴 학습 가능하지만 계산 비용이 증가한다.
recurrent_dropout = 0.25: 순환 상태 업데이트 시, 일부 뉴런을 무작위로 비활성화(Dropout)하여 과적합을 방지한다.
layer_dropout(0.5): 드롭아웃 계층
rate = 0.5: 전체 뉴런의 50%를 무작위로 비활성화하여 과적합을 방지한다. layer_dense(units = 1): Dense 계층
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
# 3. Bidirection LSTM set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% bidirectional (layer_lstm (units = 16 )) %>% layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_4"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_5 (InputLayer) [(None, 12, 12)] 0
bidirectional (Bidirectional) (None, 32) 3712
dense_5 (Dense) (None, 1) 33
========================================================================================================================================================================================================
Total params: 3745 (14.63 KB)
Trainable params: 3745 (14.63 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
bidirectional(layer_lstm(units = 16)): 양방향 LSTM 계층
bidirectional: LSTM을 Input의 앞방향(Forward)과 뒤방향(Backward)으로 학습시킨다.layer_lstm(units = 16)
LSTM 계층의 출력 공간의 차원은 16이다.
양방향 학습으로 인해, 최종 출력은 앞방향 출력(16차원)과 뒤방향 출력(16차원)을 합쳐 32차원의 벡터이다.
양방향 구조는 Input의 문맥 정보(앞뒤 관계)를 더 잘 포착할 수 있도록 돕는다.
layer_dense(units = 1): Dense 계층
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
Gated Recurrent Unit (GRU)
# 1. Simple GRU set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% layer_gru (units = 32 , recurrent_dropout = 0.5 , return_sequences = TRUE ) %>% # 모든 시점(Time Step)에 대해서 은닉 상태값을 출력 layer_gru (units = 32 , recurrent_dropout = 0.5 ) %>% layer_dropout (0.5 ) %>% layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_5"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_6 (InputLayer) [(None, 12, 12)] 0
gru_1 (GRU) (None, 12, 32) 4416
gru (GRU) (None, 32) 6336
dropout_1 (Dropout) (None, 32) 0
dense_6 (Dense) (None, 1) 33
========================================================================================================================================================================================================
Total params: 10785 (42.13 KB)
Trainable params: 10785 (42.13 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
layer_gru(units = 32, recurrent_dropout = 0.5, return_sequences = TRUE): GRU 계층
units = 32: GRU 계층이 출력할 은닉 상태(Hidden State)의 차원은 32이다.
이는 GRU가 학습하는 표현 공간의 크기를 의미한다.
recurrent_dropout = 0.5: 순환 상태 업데이트 시, 50%의 뉴런을 무작위로 비활성화하여 과적합을 방지한다.return_sequences = TRUE: 모든 시점(Time Step)에 대한 은닉 상태 출력을 반환한다.
GRU와 LSTM 모두 다중 계층으로 쌓을 경우 옵션 return_sequences = TRUE이 필요하다.
layer_dropout(0.5): 드롭아웃 계층
rate = 0.5: 모든 출력 값 중 50%를 무작위로 비활성화하여 과적합을 방지한다. layer_dense(units = 1): Dense 계층
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
# 2. Bidirection GRU set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% bidirectional (layer_gru (units = 16 )) %>% layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_6"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_7 (InputLayer) [(None, 12, 12)] 0
bidirectional_1 (Bidirectional) (None, 32) 2880
dense_7 (Dense) (None, 1) 33
========================================================================================================================================================================================================
Total params: 2913 (11.38 KB)
Trainable params: 2913 (11.38 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
bidirectional(layer_gru(units = 16)): 양방향 GRU 계층
bidirectional: GRU 계층을 양방향으로 학습시킨다.
앞방향(Forward): 입력 시퀀스를 처음부터 끝까지 처리한다.
뒤방향(Backward): 입력 시퀀스를 끝에서 처음까지 처리한다.
각 방향에서 얻어진 결과를 결합하여 더 풍부한 시퀀스 정보 학습 가능하다.
layer_gru(units = 16)
GRU 계층의 출력 공간 차원은 16이다.
양방향 학습을 적용하면 최종 출력의 차원은 앞방향(16) + 뒤방향(16) = 32이다.
layer_dense(units = 1): Dense 계층 추가
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
CNN 1D + GRU
set.seed (100 )<- layer_input (shape = c (sequence_length, ncol_input_data)) <- inputs %>% layer_conv_1d (filters = 32 , kernel_size = 6 , activation = "relu" ) %>% layer_max_pooling_1d (pool_size = 2 ) %>% layer_conv_1d (filters = 32 , kernel_size = 3 , activation = "relu" ) %>% layer_gru (units = 32 , recurrent_dropout = 0.5 , return_sequences = TRUE ) %>% layer_dropout (0.1 ) %>% layer_dense (units = 1 ) # Default: Linear Activation <- keras_model (inputs, outputs)summary (model)
Model: "model_7"
________________________________________________________________________________________________________________________________________________________________________________________________________
Layer (type) Output Shape Param #
========================================================================================================================================================================================================
input_8 (InputLayer) [(None, 12, 12)] 0
conv1d_3 (Conv1D) (None, 7, 32) 2336
max_pooling1d_1 (MaxPooling1D) (None, 3, 32) 0
conv1d_2 (Conv1D) (None, 1, 32) 3104
gru_3 (GRU) (None, 1, 32) 6336
dropout_2 (Dropout) (None, 1, 32) 0
dense_8 (Dense) (None, 1, 1) 33
========================================================================================================================================================================================================
Total params: 11809 (46.13 KB)
Trainable params: 11809 (46.13 KB)
Non-trainable params: 0 (0.00 Byte)
________________________________________________________________________________________________________________________________________________________________________________________________________
코드 설명
layer_conv_1d(filters = 32, kernel_size = 6, activation = "relu"): 1D 컨볼루션 계층
filters: 콘벌루션 필터 개수를 입력한다.
필터 수가 많을수록 더 복잡한 특징을 학습할 수 있지만 계산 비용 증가한다.
kernel_size: 모형이 학습할 데이터 패턴의 시간적 범위(시계열 윈도우 크기)를 결정한다.activation: 활성화 함수를 입력한다. layer_max_pooling_1d(pool_size = 2): 1D Max Pooling 계층 → 시계열 데이터의 차원을 축소
pool_size(= Max Pooling Window Length)를 “2”로 지정한다.strides의 경우 옵션 pool_size에 입력한 값이 Default(여기서는 2)이다.두 옵션을 통해 해당 계층에서 입력 데이터의 차원을 절반으로 축소한다.
함수 layer_max_pooling_1d() 다음에 입력한 함수 layer_conv_1d()의 옵션 kernel_size는 절반으로 축소한 “3”으로 지정한다.
layer_gru(units = 32, recurrent_dropout = 0.5, return_sequences = TRUE): GRU 계층
units = 32: GRU 계층의 출력 공간 차원은 32차원이다.
시계열 데이터를 압축된 32차원 벡터로 표현.
recurrent_dropout = 0.5: 순환 상태 업데이트 시 50% 뉴런을 무작위로 비활성화하여 과적합 방지한다.return_sequences = TRUE: 모든 시점(Time Step)에 대한 은닉 상태 출력을 반환한다.
이 출력은 다음 계층(드롭아웃 계층)에서 사용된다.
layer_dropout(0.1): 드롭아웃 계층
rate = 0.1: 전체 뉴런 중 10%를 무작위로 비활성화하여 과적합을 방지한다. layer_dense(units = 1): Dense 계층
회귀 문제(연속형 값 예측)를 해결하기 위해 units = 1로 설정한다.
활성화 함수가 지정되지 않았으므로 선형 활성화 함수(Linear Activation)를 사용한다.
Model Compile
%>% compile (optimizer = "rmsprop" ,loss = "mse" ,metrics = "mae" )
Model Fit
<- model %>% fit (train_dataset,epochs = 100 ,validation_data = val_dataset,callbacks = callbacks_list)
Epoch 1/100
4/4 - 3s - loss: 3015755.5000 - mae: 1729.6298 - val_loss: 3510547.5000 - val_mae: 1867.4125 - lr: 0.0010 - 3s/epoch - 670ms/step
Epoch 2/100
4/4 - 0s - loss: 3011951.5000 - mae: 1728.5303 - val_loss: 3506447.2500 - val_mae: 1866.3142 - lr: 0.0010 - 143ms/epoch - 36ms/step
Epoch 3/100
4/4 - 0s - loss: 3008031.5000 - mae: 1727.3945 - val_loss: 3502763.7500 - val_mae: 1865.3269 - lr: 0.0010 - 110ms/epoch - 27ms/step
Epoch 4/100
4/4 - 0s - loss: 3004926.5000 - mae: 1726.4961 - val_loss: 3499602.5000 - val_mae: 1864.4791 - lr: 0.0010 - 105ms/epoch - 26ms/step
Epoch 5/100
4/4 - 0s - loss: 3002021.5000 - mae: 1725.6591 - val_loss: 3496844.7500 - val_mae: 1863.7393 - lr: 0.0010 - 107ms/epoch - 27ms/step
Epoch 6/100
4/4 - 0s - loss: 2999773.0000 - mae: 1725.0037 - val_loss: 3494691.7500 - val_mae: 1863.1616 - lr: 0.0010 - 102ms/epoch - 26ms/step
Epoch 7/100
4/4 - 0s - loss: 2997919.0000 - mae: 1724.4734 - val_loss: 3492967.7500 - val_mae: 1862.6989 - lr: 0.0010 - 105ms/epoch - 26ms/step
Epoch 8/100
4/4 - 0s - loss: 2996537.0000 - mae: 1724.0734 - val_loss: 3491554.7500 - val_mae: 1862.3195 - lr: 0.0010 - 113ms/epoch - 28ms/step
Epoch 9/100
4/4 - 0s - loss: 2995356.2500 - mae: 1723.7346 - val_loss: 3490382.0000 - val_mae: 1862.0045 - lr: 0.0010 - 106ms/epoch - 26ms/step
Epoch 10/100
4/4 - 0s - loss: 2993795.0000 - mae: 1723.2834 - val_loss: 3489416.7500 - val_mae: 1861.7454 - lr: 0.0010 - 108ms/epoch - 27ms/step
Epoch 11/100
4/4 - 0s - loss: 2993752.2500 - mae: 1723.2705 - val_loss: 3488636.0000 - val_mae: 1861.5358 - lr: 0.0010 - 110ms/epoch - 27ms/step
Epoch 12/100
4/4 - 0s - loss: 2992527.0000 - mae: 1722.9133 - val_loss: 3487957.7500 - val_mae: 1861.3534 - lr: 0.0010 - 110ms/epoch - 27ms/step
Epoch 13/100
4/4 - 0s - loss: 2991723.5000 - mae: 1722.6765 - val_loss: 3487336.5000 - val_mae: 1861.1865 - lr: 0.0010 - 117ms/epoch - 29ms/step
Epoch 14/100
4/4 - 0s - loss: 2991444.0000 - mae: 1722.5984 - val_loss: 3486740.2500 - val_mae: 1861.0264 - lr: 0.0010 - 111ms/epoch - 28ms/step
Epoch 15/100
4/4 - 0s - loss: 2990621.0000 - mae: 1722.3628 - val_loss: 3486084.5000 - val_mae: 1860.8502 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 16/100
4/4 - 0s - loss: 2990892.5000 - mae: 1722.4348 - val_loss: 3485462.0000 - val_mae: 1860.6829 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 17/100
4/4 - 0s - loss: 2989982.5000 - mae: 1722.1741 - val_loss: 3484911.5000 - val_mae: 1860.5350 - lr: 0.0010 - 108ms/epoch - 27ms/step
Epoch 18/100
4/4 - 0s - loss: 2989754.5000 - mae: 1722.1096 - val_loss: 3484394.7500 - val_mae: 1860.3961 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 19/100
4/4 - 0s - loss: 2988716.7500 - mae: 1721.8124 - val_loss: 3483891.0000 - val_mae: 1860.2607 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 20/100
4/4 - 0s - loss: 2988231.0000 - mae: 1721.6699 - val_loss: 3483394.7500 - val_mae: 1860.1274 - lr: 0.0010 - 100ms/epoch - 25ms/step
Epoch 21/100
4/4 - 0s - loss: 2987860.5000 - mae: 1721.5620 - val_loss: 3482908.2500 - val_mae: 1859.9966 - lr: 0.0010 - 100ms/epoch - 25ms/step
Epoch 22/100
4/4 - 0s - loss: 2987233.0000 - mae: 1721.3765 - val_loss: 3482422.5000 - val_mae: 1859.8661 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 23/100
4/4 - 0s - loss: 2987370.7500 - mae: 1721.4136 - val_loss: 3481946.0000 - val_mae: 1859.7379 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 24/100
4/4 - 0s - loss: 2986856.0000 - mae: 1721.2600 - val_loss: 3481468.2500 - val_mae: 1859.6096 - lr: 0.0010 - 114ms/epoch - 28ms/step
Epoch 25/100
4/4 - 0s - loss: 2985938.5000 - mae: 1721.0059 - val_loss: 3480990.5000 - val_mae: 1859.4812 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 26/100
4/4 - 0s - loss: 2985030.7500 - mae: 1720.7338 - val_loss: 3480509.0000 - val_mae: 1859.3516 - lr: 0.0010 - 102ms/epoch - 25ms/step
Epoch 27/100
4/4 - 0s - loss: 2985316.5000 - mae: 1720.8207 - val_loss: 3480035.7500 - val_mae: 1859.2242 - lr: 0.0010 - 101ms/epoch - 25ms/step
Epoch 28/100
4/4 - 0s - loss: 2985155.7500 - mae: 1720.7756 - val_loss: 3479565.0000 - val_mae: 1859.0977 - lr: 0.0010 - 101ms/epoch - 25ms/step
Epoch 29/100
4/4 - 0s - loss: 2984509.0000 - mae: 1720.5854 - val_loss: 3479091.5000 - val_mae: 1858.9703 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 30/100
4/4 - 0s - loss: 2984135.5000 - mae: 1720.4786 - val_loss: 3478618.2500 - val_mae: 1858.8430 - lr: 0.0010 - 109ms/epoch - 27ms/step
Epoch 31/100
4/4 - 0s - loss: 2983686.0000 - mae: 1720.3494 - val_loss: 3478145.2500 - val_mae: 1858.7158 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 32/100
4/4 - 0s - loss: 2983551.7500 - mae: 1720.3069 - val_loss: 3477675.0000 - val_mae: 1858.5892 - lr: 0.0010 - 105ms/epoch - 26ms/step
Epoch 33/100
4/4 - 0s - loss: 2982203.5000 - mae: 1719.9174 - val_loss: 3477195.2500 - val_mae: 1858.4601 - lr: 0.0010 - 101ms/epoch - 25ms/step
Epoch 34/100
4/4 - 0s - loss: 2982147.2500 - mae: 1719.8997 - val_loss: 3476721.7500 - val_mae: 1858.3330 - lr: 0.0010 - 101ms/epoch - 25ms/step
Epoch 35/100
4/4 - 0s - loss: 2981973.5000 - mae: 1719.8481 - val_loss: 3476249.7500 - val_mae: 1858.2058 - lr: 0.0010 - 100ms/epoch - 25ms/step
Epoch 36/100
4/4 - 0s - loss: 2981239.0000 - mae: 1719.6362 - val_loss: 3475774.0000 - val_mae: 1858.0778 - lr: 0.0010 - 101ms/epoch - 25ms/step
Epoch 37/100
4/4 - 0s - loss: 2980859.0000 - mae: 1719.5327 - val_loss: 3475302.0000 - val_mae: 1857.9507 - lr: 0.0010 - 106ms/epoch - 27ms/step
Epoch 38/100
4/4 - 0s - loss: 2980679.0000 - mae: 1719.4746 - val_loss: 3474832.2500 - val_mae: 1857.8245 - lr: 0.0010 - 137ms/epoch - 34ms/step
Epoch 39/100
4/4 - 0s - loss: 2980071.0000 - mae: 1719.2957 - val_loss: 3474356.0000 - val_mae: 1857.6963 - lr: 0.0010 - 118ms/epoch - 29ms/step
Epoch 40/100
4/4 - 0s - loss: 2979003.0000 - mae: 1718.9803 - val_loss: 3473879.0000 - val_mae: 1857.5677 - lr: 0.0010 - 107ms/epoch - 27ms/step
Epoch 41/100
4/4 - 0s - loss: 2978961.0000 - mae: 1718.9763 - val_loss: 3473404.7500 - val_mae: 1857.4402 - lr: 0.0010 - 111ms/epoch - 28ms/step
Epoch 42/100
4/4 - 0s - loss: 2978741.5000 - mae: 1718.9108 - val_loss: 3472931.5000 - val_mae: 1857.3129 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 43/100
4/4 - 0s - loss: 2978480.5000 - mae: 1718.8389 - val_loss: 3472461.2500 - val_mae: 1857.1862 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 44/100
4/4 - 0s - loss: 2977611.0000 - mae: 1718.5801 - val_loss: 3471985.2500 - val_mae: 1857.0579 - lr: 0.0010 - 109ms/epoch - 27ms/step
Epoch 45/100
4/4 - 0s - loss: 2977508.2500 - mae: 1718.5557 - val_loss: 3471512.7500 - val_mae: 1856.9307 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 46/100
4/4 - 0s - loss: 2976562.0000 - mae: 1718.2742 - val_loss: 3471039.2500 - val_mae: 1856.8033 - lr: 0.0010 - 106ms/epoch - 26ms/step
Epoch 47/100
4/4 - 0s - loss: 2976689.0000 - mae: 1718.3075 - val_loss: 3470570.0000 - val_mae: 1856.6769 - lr: 0.0010 - 110ms/epoch - 27ms/step
Epoch 48/100
4/4 - 0s - loss: 2976037.0000 - mae: 1718.1287 - val_loss: 3470096.2500 - val_mae: 1856.5493 - lr: 0.0010 - 153ms/epoch - 38ms/step
Epoch 49/100
4/4 - 0s - loss: 2975215.5000 - mae: 1717.8835 - val_loss: 3469620.5000 - val_mae: 1856.4211 - lr: 0.0010 - 109ms/epoch - 27ms/step
Epoch 50/100
4/4 - 0s - loss: 2975328.0000 - mae: 1717.9236 - val_loss: 3469149.5000 - val_mae: 1856.2942 - lr: 0.0010 - 101ms/epoch - 25ms/step
Epoch 51/100
4/4 - 0s - loss: 2974362.5000 - mae: 1717.6335 - val_loss: 3468673.7500 - val_mae: 1856.1661 - lr: 0.0010 - 105ms/epoch - 26ms/step
Epoch 52/100
4/4 - 0s - loss: 2974627.0000 - mae: 1717.7124 - val_loss: 3468205.0000 - val_mae: 1856.0399 - lr: 0.0010 - 100ms/epoch - 25ms/step
Epoch 53/100
4/4 - 0s - loss: 2973422.0000 - mae: 1717.3574 - val_loss: 3467730.0000 - val_mae: 1855.9119 - lr: 0.0010 - 106ms/epoch - 26ms/step
Epoch 54/100
4/4 - 0s - loss: 2973426.5000 - mae: 1717.3634 - val_loss: 3467259.0000 - val_mae: 1855.7852 - lr: 0.0010 - 113ms/epoch - 28ms/step
Epoch 55/100
4/4 - 0s - loss: 2972886.0000 - mae: 1717.2109 - val_loss: 3466784.7500 - val_mae: 1855.6572 - lr: 0.0010 - 112ms/epoch - 28ms/step
Epoch 56/100
4/4 - 0s - loss: 2972549.7500 - mae: 1717.1045 - val_loss: 3466313.7500 - val_mae: 1855.5303 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 57/100
4/4 - 0s - loss: 2972050.5000 - mae: 1716.9619 - val_loss: 3465840.2500 - val_mae: 1855.4028 - lr: 0.0010 - 102ms/epoch - 25ms/step
Epoch 58/100
4/4 - 0s - loss: 2971238.5000 - mae: 1716.7275 - val_loss: 3465365.2500 - val_mae: 1855.2747 - lr: 0.0010 - 103ms/epoch - 26ms/step
Epoch 59/100
4/4 - 0s - loss: 2971871.2500 - mae: 1716.9055 - val_loss: 3464897.0000 - val_mae: 1855.1484 - lr: 0.0010 - 108ms/epoch - 27ms/step
Epoch 60/100
4/4 - 0s - loss: 2970549.2500 - mae: 1716.5258 - val_loss: 3464422.7500 - val_mae: 1855.0206 - lr: 0.0010 - 136ms/epoch - 34ms/step
Epoch 61/100
4/4 - 0s - loss: 2970675.0000 - mae: 1716.5710 - val_loss: 3463953.0000 - val_mae: 1854.8940 - lr: 0.0010 - 110ms/epoch - 27ms/step
Epoch 62/100
4/4 - 0s - loss: 2970028.0000 - mae: 1716.3696 - val_loss: 3463480.2500 - val_mae: 1854.7666 - lr: 0.0010 - 117ms/epoch - 29ms/step
Epoch 63/100
4/4 - 0s - loss: 2969632.0000 - mae: 1716.2531 - val_loss: 3463010.0000 - val_mae: 1854.6398 - lr: 0.0010 - 120ms/epoch - 30ms/step
Epoch 64/100
4/4 - 0s - loss: 2969028.5000 - mae: 1716.0813 - val_loss: 3462535.7500 - val_mae: 1854.5121 - lr: 0.0010 - 105ms/epoch - 26ms/step
Epoch 65/100
4/4 - 0s - loss: 2968761.5000 - mae: 1716.0060 - val_loss: 3462064.7500 - val_mae: 1854.3851 - lr: 0.0010 - 104ms/epoch - 26ms/step
Epoch 66/100
4/4 - 0s - loss: 2967757.0000 - mae: 1715.7211 - val_loss: 3461590.0000 - val_mae: 1854.2570 - lr: 0.0010 - 109ms/epoch - 27ms/step
Epoch 67/100
4/4 - 0s - loss: 2967677.7500 - mae: 1715.6912 - val_loss: 3461116.5000 - val_mae: 1854.1294 - lr: 0.0010 - 119ms/epoch - 30ms/step
Epoch 68/100
4/4 - 0s - loss: 2967094.5000 - mae: 1715.5277 - val_loss: 3460642.7500 - val_mae: 1854.0016 - lr: 0.0010 - 119ms/epoch - 30ms/step
Epoch 69/100
4/4 - 0s - loss: 2966265.7500 - mae: 1715.2784 - val_loss: 3460166.0000 - val_mae: 1853.8732 - lr: 0.0010 - 124ms/epoch - 31ms/step
Epoch 70/100
4/4 - 0s - loss: 2966430.7500 - mae: 1715.3225 - val_loss: 3459696.0000 - val_mae: 1853.7463 - lr: 0.0010 - 105ms/epoch - 26ms/step
Epoch 71/100
4/4 - 0s - loss: 2965965.7500 - mae: 1715.1929 - val_loss: 3459226.0000 - val_mae: 1853.6195 - lr: 0.0010 - 106ms/epoch - 26ms/step
Epoch 72/100
4/4 - 0s - loss: 2965601.5000 - mae: 1715.0746 - val_loss: 3458754.7500 - val_mae: 1853.4924 - lr: 0.0010 - 108ms/epoch - 27ms/step
Epoch 73/100
4/4 - 0s - loss: 2965912.5000 - mae: 1715.1731 - val_loss: 3458287.0000 - val_mae: 1853.3662 - lr: 0.0010 - 110ms/epoch - 27ms/step
Epoch 74/100
4/4 - 0s - loss: 2964489.0000 - mae: 1714.7600 - val_loss: 3457813.2500 - val_mae: 1853.2383 - lr: 0.0010 - 106ms/epoch - 26ms/step
Epoch 75/100
4/4 - 0s - loss: 2964205.5000 - mae: 1714.6759 - val_loss: 3457341.0000 - val_mae: 1853.1108 - lr: 0.0010 - 136ms/epoch - 34ms/step
Epoch 76/100
4/4 - 0s - loss: 2963915.7500 - mae: 1714.5992 - val_loss: 3456870.0000 - val_mae: 1852.9839 - lr: 0.0010 - 121ms/epoch - 30ms/step
Epoch 77/100
4/4 - 0s - loss: 2963873.0000 - mae: 1714.5830 - val_loss: 3456401.0000 - val_mae: 1852.8572 - lr: 0.0010 - 114ms/epoch - 28ms/step
Epoch 78/100
4/4 - 0s - loss: 2963063.0000 - mae: 1714.3423 - val_loss: 3455927.5000 - val_mae: 1852.7295 - lr: 0.0010 - 109ms/epoch - 27ms/step
Epoch 79/100
4/4 - 0s - loss: 2962893.5000 - mae: 1714.2915 - val_loss: 3455456.0000 - val_mae: 1852.6023 - lr: 0.0010 - 107ms/epoch - 27ms/step
Epoch 80/100
4/4 - 0s - loss: 2961861.5000 - mae: 1713.9924 - val_loss: 3454981.5000 - val_mae: 1852.4741 - lr: 0.0010 - 118ms/epoch - 30ms/step
Epoch 81/100
4/4 - 0s - loss: 2961676.0000 - mae: 1713.9305 - val_loss: 3454507.5000 - val_mae: 1852.3463 - lr: 0.0010 - 118ms/epoch - 29ms/step
Epoch 82/100
4/4 - 0s - loss: 2962104.7500 - mae: 1714.0554 - val_loss: 3454041.0000 - val_mae: 1852.2202 - lr: 0.0010 - 163ms/epoch - 41ms/step
Epoch 83/100
4/4 - 0s - loss: 2960754.2500 - mae: 1713.6653 - val_loss: 3453566.5000 - val_mae: 1852.0923 - lr: 0.0010 - 132ms/epoch - 33ms/step
Epoch 84/100
4/4 - 0s - loss: 2960101.0000 - mae: 1713.4835 - val_loss: 3453092.5000 - val_mae: 1851.9642 - lr: 0.0010 - 112ms/epoch - 28ms/step
Epoch 85/100
4/4 - 0s - loss: 2960013.2500 - mae: 1713.4487 - val_loss: 3452621.2500 - val_mae: 1851.8369 - lr: 0.0010 - 111ms/epoch - 28ms/step
Epoch 86/100
4/4 - 0s - loss: 2959677.7500 - mae: 1713.3535 - val_loss: 3452150.2500 - val_mae: 1851.7100 - lr: 0.0010 - 157ms/epoch - 39ms/step
Epoch 87/100
4/4 - 0s - loss: 2958939.7500 - mae: 1713.1428 - val_loss: 3451677.7500 - val_mae: 1851.5823 - lr: 0.0010 - 113ms/epoch - 28ms/step
Epoch 88/100
4/4 - 0s - loss: 2958942.2500 - mae: 1713.1335 - val_loss: 3451208.7500 - val_mae: 1851.4557 - lr: 0.0010 - 118ms/epoch - 29ms/step
Epoch 89/100
4/4 - 0s - loss: 2957843.5000 - mae: 1712.8151 - val_loss: 3450735.2500 - val_mae: 1851.3278 - lr: 0.0010 - 160ms/epoch - 40ms/step
Epoch 90/100
4/4 - 0s - loss: 2957929.7500 - mae: 1712.8333 - val_loss: 3450264.7500 - val_mae: 1851.2006 - lr: 0.0010 - 123ms/epoch - 31ms/step
Epoch 91/100
4/4 - 0s - loss: 2957277.2500 - mae: 1712.6523 - val_loss: 3449792.2500 - val_mae: 1851.0731 - lr: 0.0010 - 121ms/epoch - 30ms/step
Epoch 92/100
4/4 - 0s - loss: 2957049.0000 - mae: 1712.5824 - val_loss: 3449321.0000 - val_mae: 1850.9458 - lr: 0.0010 - 115ms/epoch - 29ms/step
Epoch 93/100
4/4 - 0s - loss: 2955694.5000 - mae: 1712.1943 - val_loss: 3448846.0000 - val_mae: 1850.8174 - lr: 0.0010 - 121ms/epoch - 30ms/step
Epoch 94/100
4/4 - 0s - loss: 2955342.2500 - mae: 1712.0889 - val_loss: 3448371.2500 - val_mae: 1850.6891 - lr: 0.0010 - 115ms/epoch - 29ms/step
Epoch 95/100
4/4 - 0s - loss: 2955005.5000 - mae: 1711.9946 - val_loss: 3447898.7500 - val_mae: 1850.5615 - lr: 0.0010 - 120ms/epoch - 30ms/step
Epoch 96/100
4/4 - 0s - loss: 2955957.0000 - mae: 1712.2617 - val_loss: 3447433.5000 - val_mae: 1850.4358 - lr: 0.0010 - 113ms/epoch - 28ms/step
Epoch 97/100
4/4 - 0s - loss: 2954982.5000 - mae: 1711.9825 - val_loss: 3446963.7500 - val_mae: 1850.3088 - lr: 0.0010 - 115ms/epoch - 29ms/step
Epoch 98/100
4/4 - 0s - loss: 2954086.7500 - mae: 1711.7157 - val_loss: 3446490.0000 - val_mae: 1850.1808 - lr: 0.0010 - 118ms/epoch - 29ms/step
Epoch 99/100
4/4 - 0s - loss: 2953425.2500 - mae: 1711.5334 - val_loss: 3446017.7500 - val_mae: 1850.0532 - lr: 0.0010 - 112ms/epoch - 28ms/step
Epoch 100/100
4/4 - 0s - loss: 2953116.0000 - mae: 1711.4209 - val_loss: 3445544.7500 - val_mae: 1849.9253 - lr: 0.0010 - 111ms/epoch - 28ms/step
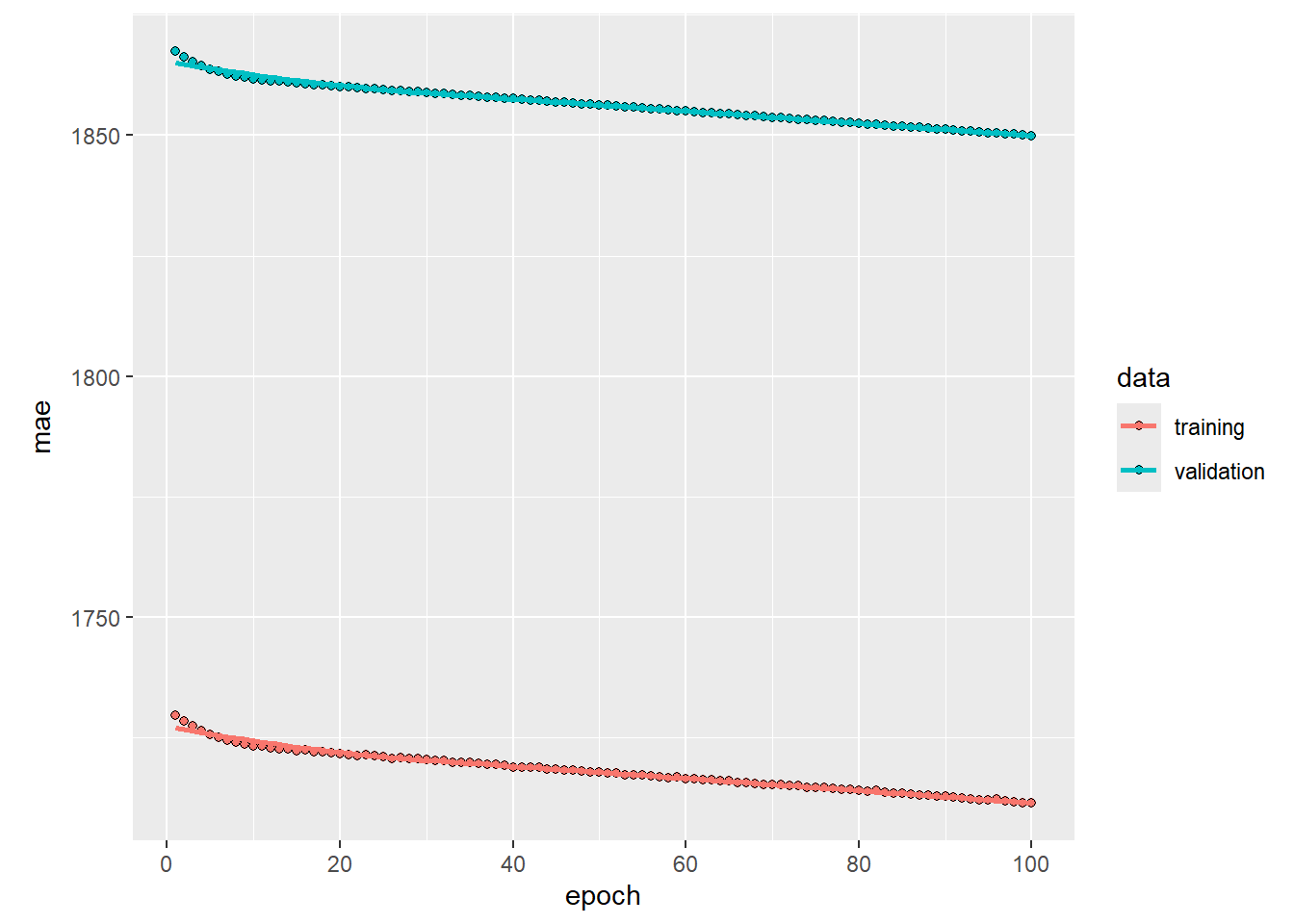
plot (history, metrics = "mae" )
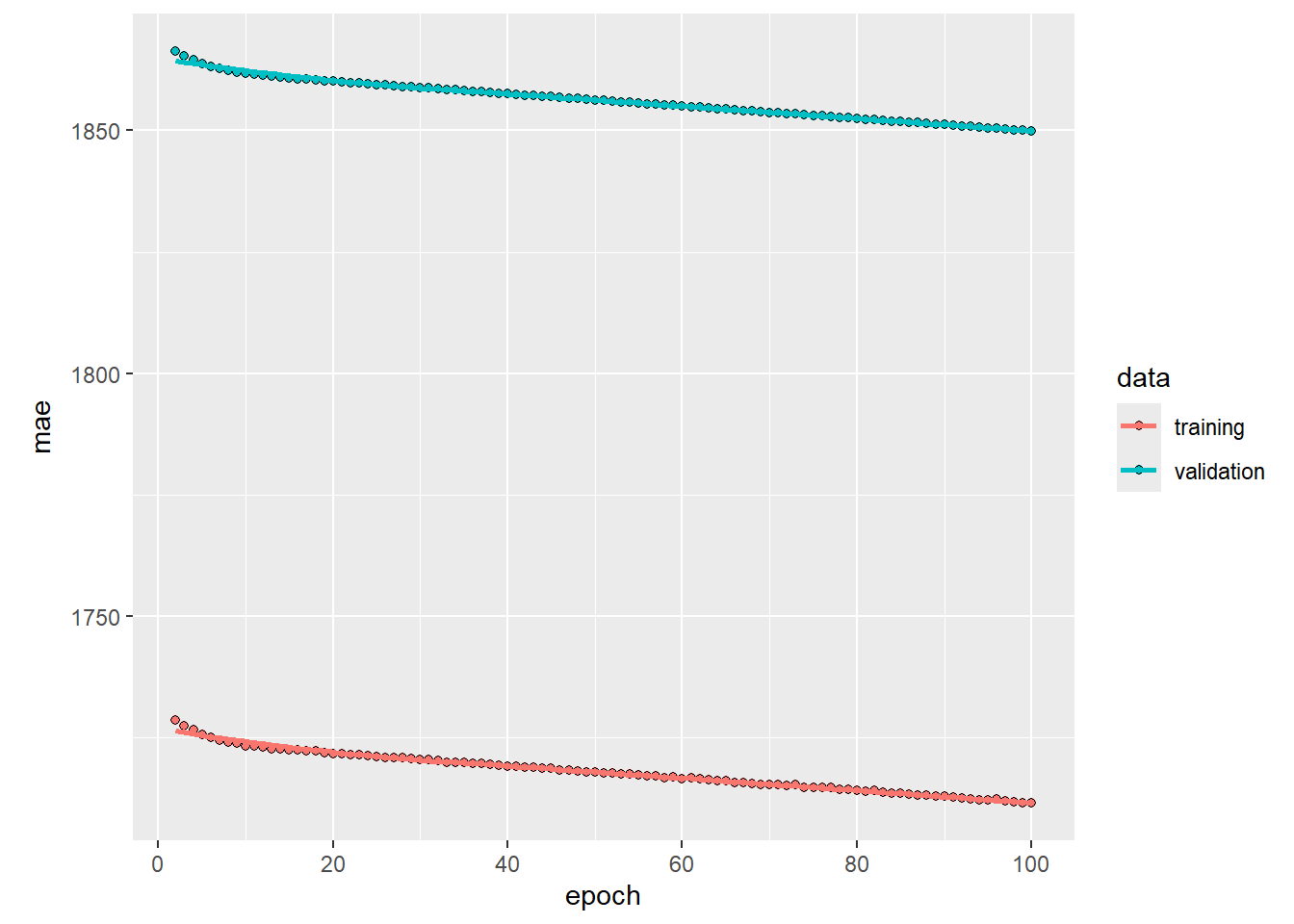
local ({<- plot (history, metrics = "mae" )$ data %<>% .[.$ epoch > 1 , ]print (p)
# 훈련된 최종 모형 저장 save_model_tf (model, filepath= "model1.keras" )
Model Evaluate
sprintf ("Test MAE: %.2f" , evaluate (model, test_dataset)["mae" ])
1/1 - 0s - loss: 3609287.5000 - mae: 1895.1899 - 58ms/epoch - 58ms/step
Prediction
함수 predict()를 이용하여 Test Dataset에 대한 예측을 수행한다.
# 훈련된 최종 모형에 대한 예측 <- model %>% predict (test_dataset) # In 3-1. test_dataset: (Input, Target) Dataset으로 분할된 TeD
1/1 - 0s - 344ms/epoch - 344ms/step
, , 1
[,1]
[1,] 18.70679
[2,] 18.70679
[3,] 18.70679
[4,] 18.70679
[5,] 18.70679
[6,] 18.70679
[7,] 18.70679
[8,] 18.70679
[9,] 18.70679
Caution! 딥러닝 기법을 시계열 데이터에 적용할 때 Training Dataset 뿐만 아니라 Test Dataset도 (Input, Target) Dataset으로 분할한다. 그리고 Test Dataset의 모든 Index에 대해 예측을 수행하는 것이 아니라 Target에 해당하는 Index에 대해서만 예측값을 생성한다.
# Best Model Loading <- load_model_tf ("Amtrack.keras" ) # 자동 저장된 Best model Loading # Best Model에 대한 예측 <- model1 %>% predict (test_dataset) # In 3-1. test_dataset: (Input, Target) Dataset으로 분할된 TeD
1/1 - 0s - 327ms/epoch - 327ms/step
, , 1
[,1]
[1,] 18.70679
[2,] 18.70679
[3,] 18.70679
[4,] 18.70679
[5,] 18.70679
[6,] 18.70679
[7,] 18.70679
[8,] 18.70679
[9,] 18.70679
# Actual Values Corresponding to Prediction Values <- NROW (test_df$ Ridership) - NROW (predictions) - delay <- test_df$ Ridership %>% # test_df$Ridership : Target tail (- delay) %>% # Drop First Delay Samples Because Index of Target Starts from 1+delay head (- num_last) # Drop Last 11
Caution! 위에서 언급했듯이 Test Dataset의 모든 Index에 대해 예측을 수행하는 것이 아니라 (Input, Target) Dataset으로 분할하고, Target에 해당하는 Index에 대해서만 예측값을 생성한다. 그래서 함수 predict()을 통해 생성한 예측값에 대응하는 실제값만 남겨두기 위해 위의 코드를 수행한다.
# Accuracy using MAE <- mean ( abs (predictions- test_y) )
# Accuracy using MSE <- mean ( (predictions- test_y)^ 2 )
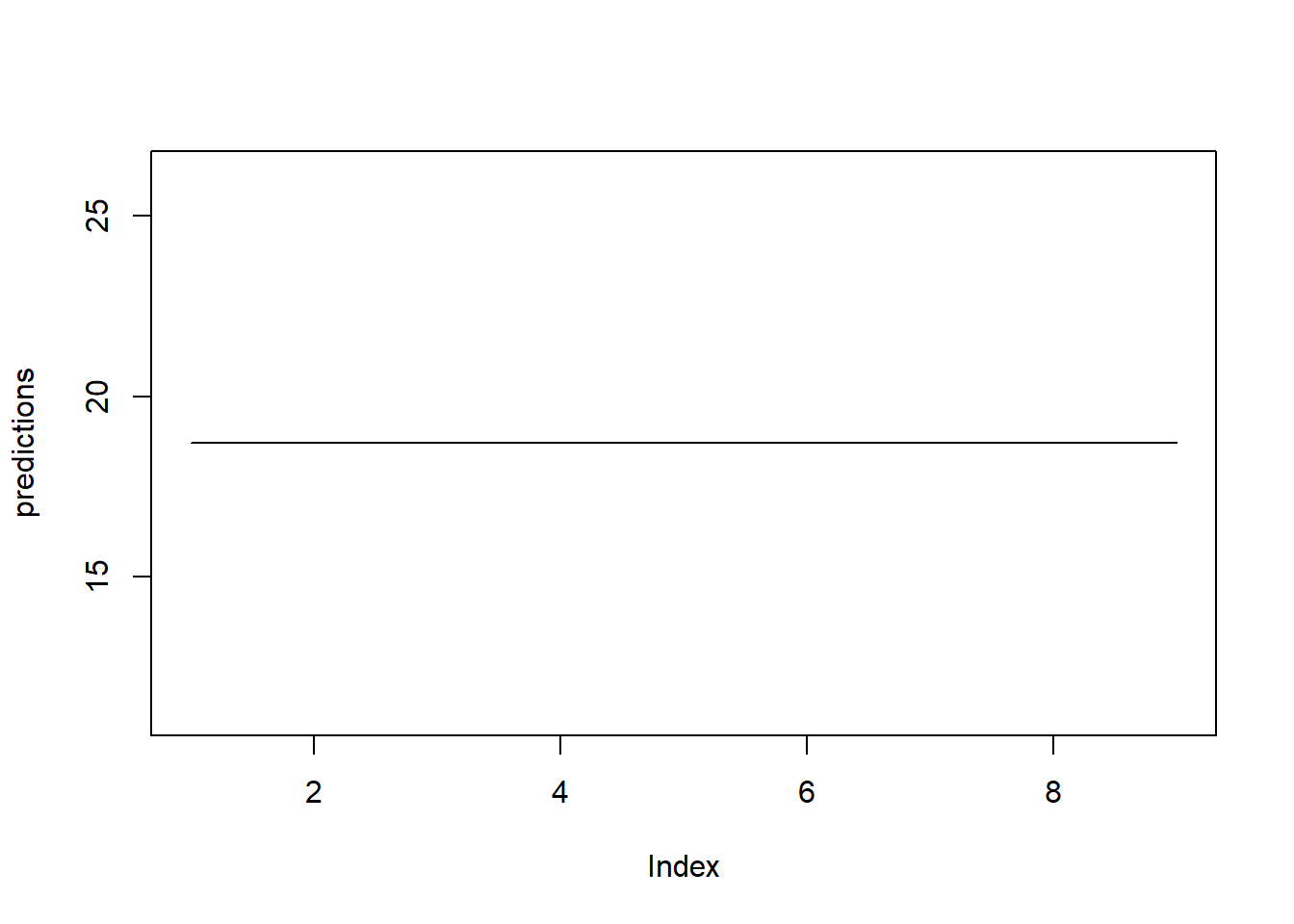
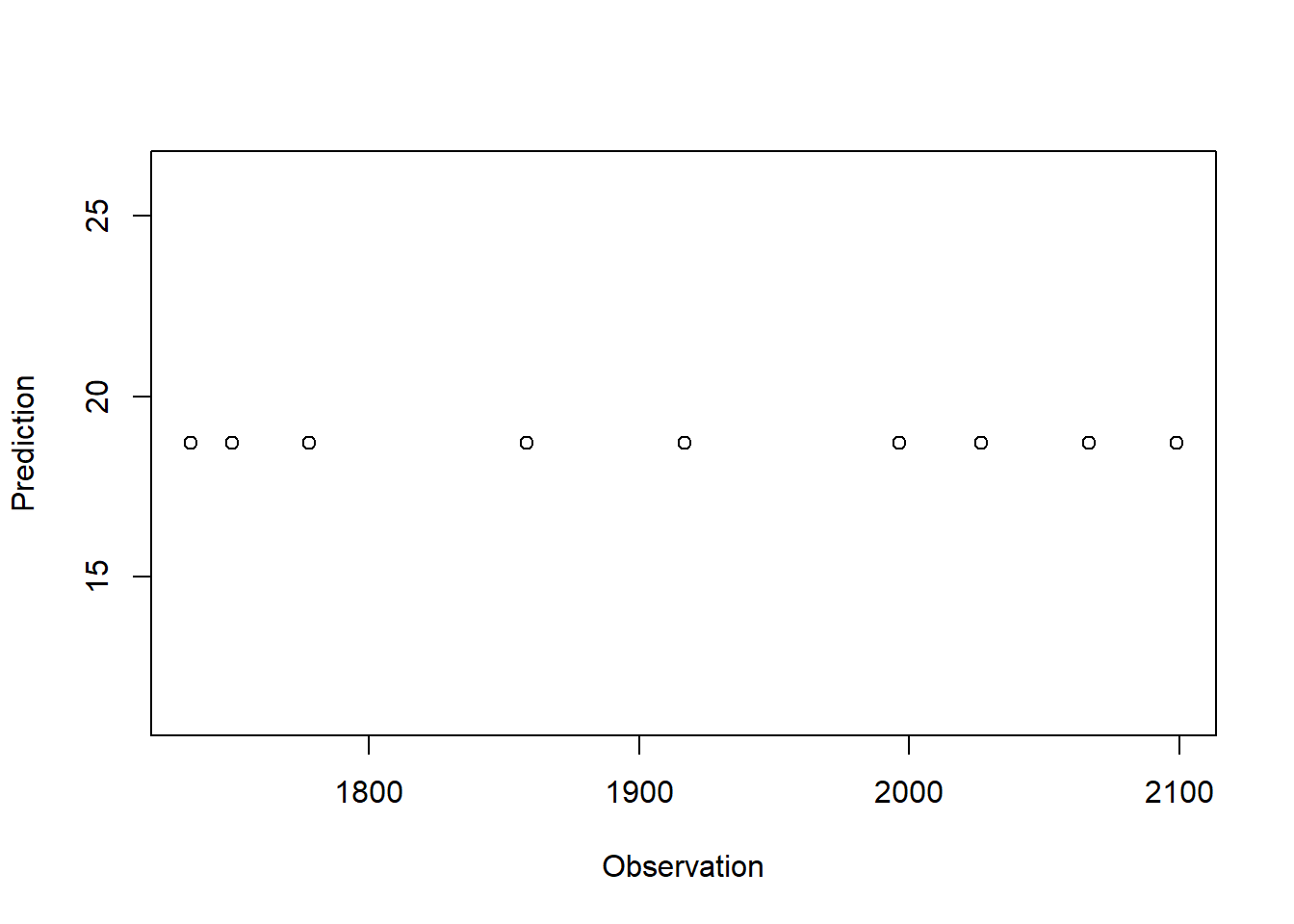
# Prediction Result Plot plot (predictions, type = "l" )lines ( test_y, col= "blue" )plot (test_y, predictions, xlab = "Observation" , ylab = "Prediction" )abline (a = 0 , b = 1 , col = "black" , lty = 2 )