14 Neural Network Model

14.1 Introduction

시계열 데이터에 신경망을 이용하여 모형 적합과 예측을 할 수 있다.
Ridership on Amtrak Trains(미국 철도 회사 “Amtrak”에서 수집한 1991년 1월~2004년 3월까지 매달 환승 고객 수) 예제를 이용하여 신경망 자기회귀모형이 실제 데이터에 어떻게 적용되는지 설명한다.

14.2 신경망

신경망은 예측변수(또는 입력값)가 밑바닥 계층을 이루고 예측값(또는 출력값)이 꼭대기 계층을 이루며 이 두 계층 중간에는 숨겨진 뉴런을 포함하는 계층이 있을 수 있다.
숨겨진 계층이 없는 경우는 선형 회귀와 같다.
아래의 그림은 4개의 예측변수를 고려하는 선형 회귀의 신경망 버전이다.

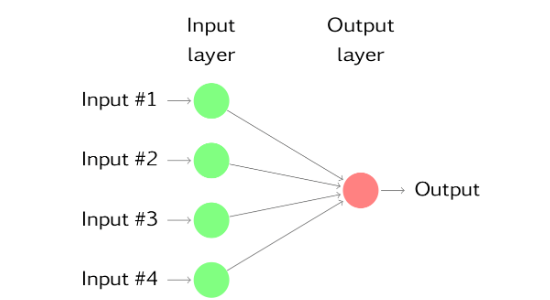
숨겨진 뉴런이 중간 계층에 있으면 신경망은 비선형이 되며 숨겨진 계층의 수와 각 숨겨진 계층의 노드 수는 반드시 미리 정해야한다.
다음 그림은 단순한 예제를 나타낸다.

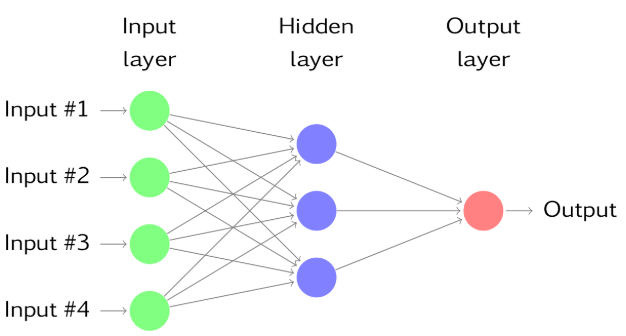
각 계층의 노드는 이전의 계층에서부터 입력값을 받는데 한 계층의 노드의 출력값은 다음 계층의 입력값이 된다.
각 마디의 입력값은 가중 선형 형태로 결합이 되며, 결과는 출력되기 전에 비선형 함수에 의해 수정된다.
- 예를 들어 위의 그림에서 숨겨진 뉴런 \(j\)로 들어가는 입력값은

\[ \begin{aligned} z_{j}=b_{j}+\sum_{i=1}^{4}\omega_{i,j}x_{i}. \end{aligned} \]

이것은 다음 계층의 입력값이 되기전 비선형 함수에 의해 수정된다.

\[ \begin{aligned} s(z)=\frac{1}{1+e^{-z}}. \end{aligned} \]

다음 계층의 노드로 들어 갈 때 각 계층의 출력값은 \(s(z)\)이며, 이것은 또 다시 가중 선형 형태로 결합되어 다음 계층의 노드의 입력값으로 들어간다.
비선형 함수로 수정됨으로써 극단적인 입력값의 효과를 줄이는 경향이 있기에 이상치에 덜 민감하다.
매개변수 \(b_{j}\), \(\omega_{i,j}\)는 data로부터 학습된 것이며 가중치의 값은 종종 너무 커지지 않도록 제한된다.
- “학습된”의 의미는 처음에는 가중치 값을 무작위로 주지만 관측된 data를 이용하여 가중치는 update된다.
- 신경망으로 출력된 예측값에는 무작위성이 있다.
- 다른 무작위 시작점을 가지고 연결망을 여러번 훈련시키고, 결과들의 평균을 구한다.

14.3 신경망 자기회귀

시계열의 시차값이 신경망의 입력값으로써 사용될 수 있으며 이것을 신경망 자기회귀 또는 NNAR 모형이라고 부른다.

14.3.1 데이터 불러오기

pacman::p_load("forecast",
               "ggplot2",
               "dplyr")

Amtrak.data <- read.csv(".../Amtrak.csv")          # 데이터 불러오기

Amtrak.data %>%
  as_tibble

# A tibble: 159 × 2
   Month      Ridership
   <chr>          <dbl>
 1 01/01/1991     1709.
 2 01/02/1991     1621.
 3 01/03/1991     1973.
 4 01/04/1991     1812.
 5 01/05/1991     1975.
 6 01/06/1991     1862.
 7 01/07/1991     1940.
 8 01/08/1991     2013.
 9 01/09/1991     1596.
10 01/10/1991     1725.
# ℹ 149 more rows

14.3.2 데이터 전처리

# Convert to ts for Target
ridership.ts <- ts(Amtrak.data$Ridership, 
                   start = c(1991, 2),            # 시계열의 시작 연도 / c(1991, 2) : 1991년 2월 -> 첫 번째 시계열은 제거했기 때문
                   frequency = 12)                # 주기 / 월별 시계열로 1년에 12번 관측


# 시계열 그림
plot(ridership.ts, 
     xlab = "Time", ylab = "Ridership (in 000s)",
     ylim = c(1300, 2300))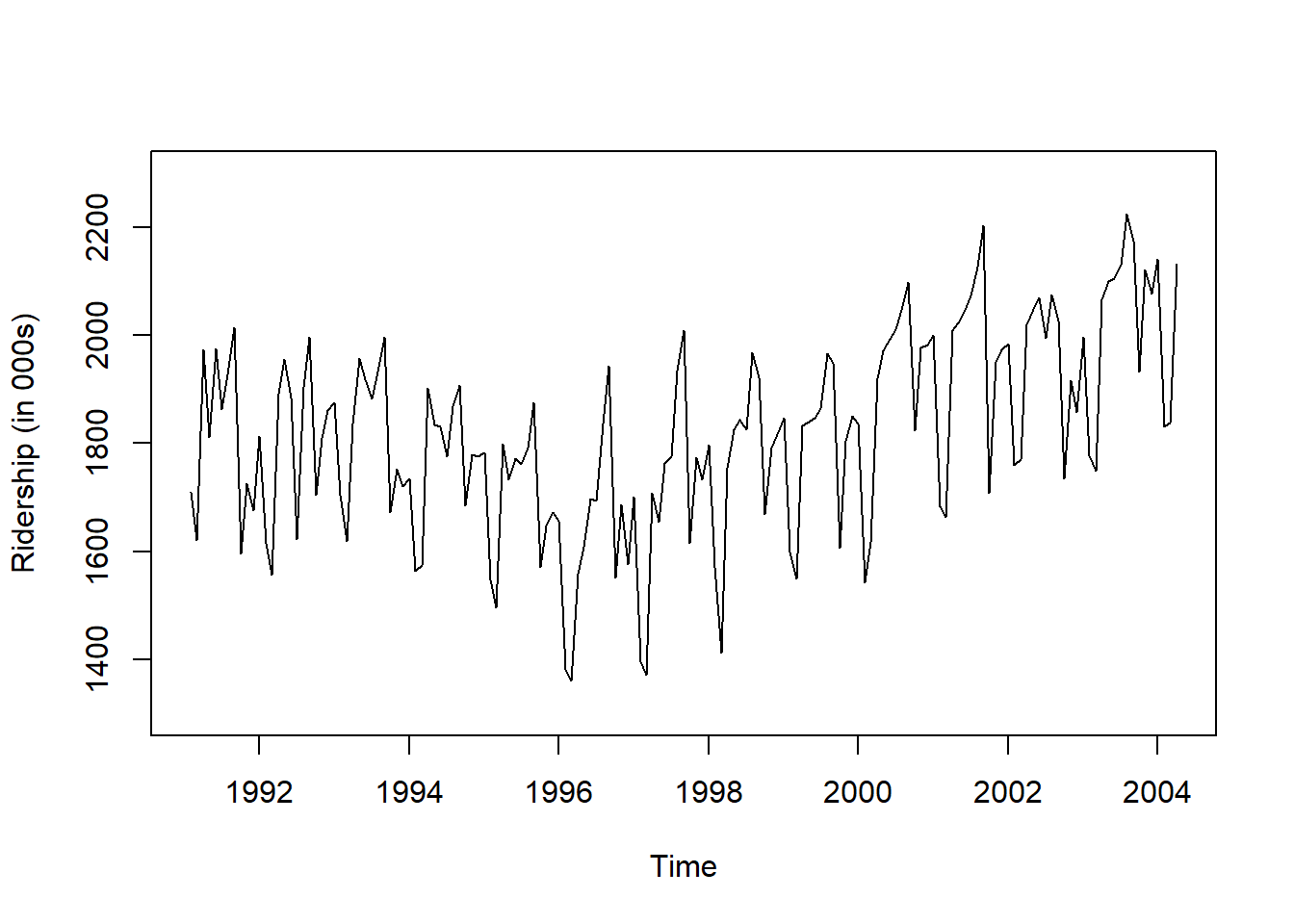

Caution! CSV 파일로 불러온 데이터를 살펴보면 승객 수를 포함하는 변수 Ridership가 수치형임을 알 수 있다. 시계열 데이터 분석을 위해 함수 ts()를 이용하여 해당 변수를 시계열 객체로 변환해야 한다.
Result! 시계열 그림을 살펴보면 Amtrak 데이터는 U자 형태의 추세를 발견할 수 있으며, 여름(7월과 8월) 동안에 승객이 급증하는 뚜렷한 계절변동도 볼 수 있다.

14.3.3 모형 적합

NNAR(\(p,k\))에서 \(p\)는 입력값으로써 사용된 시차의 수, \(k\)는 숨겨진 계층의 노드 수를 의미한다.
NNAR(\(p,k\))는 출력값 \(y_{t}\)를 예측하기 위해 마지막 \(p\)개의 관측값 (\(y_{t-1}\), \(y_{t-2}\), \(\ldots\), \(y_{t-p}\))을 입력값으로 사용하고 숨겨진 계층에 \(k\)개의 뉴런이 있는 신경망이다.
- NNAR(\(p,0\))는 ARIMA(\(p,0,0\)) 모형과 같지만 정상성을 보장하는 모수에 대한 제약이 없다. (ARIMA(\(p,0,0\)) 모형은 모수가 1보다 작아야 정상성 만족)
계절성 data에 대하여, 같은 계절의 마지막 관측값을 입력값으로 넣는 것도 유용하다.
계절성이 있는 경우 모형은 NNAR\((p,P,k)_{m}\)로써 \(P\)는 입력값으로써 사용된 계절성 시차의 수이며 \(m\)은 주기를 의미한다.
NNAR\((p,P,k)_{m}\)은 \(y_{t-1}\), \(\ldots\), \(y_{t-p}\), \(y_{t-m}\), \(y_{t-2m}\), \(\ldots\), \(y_{t-mP}\)를 입력값으로써 사용하고, 숨겨진 계층에 \(k\)개의 뉴런이 있다.
- NNAR\((p,P,k)_{m}\)은 ARIMA\((p,0,0)(P,0,0)_{m}\) 모형과 같지만 정상성을 보장하는 모수에 대한 제약이 없다.
R 함수 nnetar()은 NNAR\((p,P,k)_{m}\) 모델을 적합시키며, \(p\)와 \(P\)값들을 정하지 않으면, 자동적으로 선택된다.
- 비계절성에 대해서는 AR(\(p\)) 모형에 대하여 최적의 시차수가 기본값이다.
- 계절성 시계열에 대해서는 기본값은 \(P\)=1이고 \(p\)는 계절성으로 조정된 데이터에 맞춘 최적 선형 모델로 고른다.
- \(k\)를 정하지 않으면 \(k=(p+P+1)/2\)로 둔다. (가장 가까운 정수로 반올림)

set.seed(10)
fit <- nnetar(ridership.ts,  repeats = 200, 
              lambda = "auto")                            # If lambda="auto", then a transformation is automatically selected using BoxCox.lambda
                                                          # 200 networks to fit with different random starting weights & averaged./ Size : The number of hidden node

autoplot(forecast(fit, h = 30)) + 
  ylab("Ridership")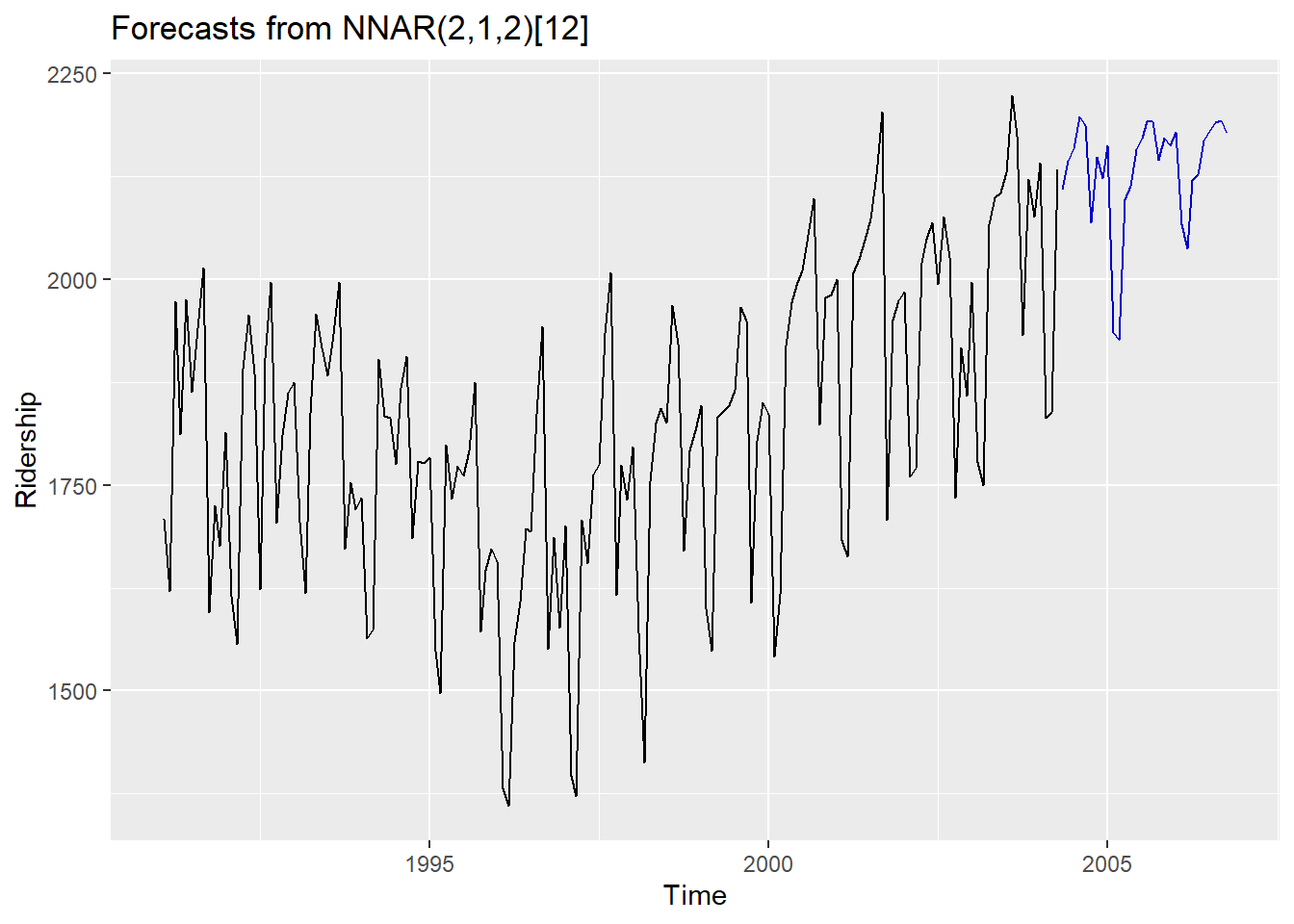

예측할 때는 연결망을 반복하여 적용한다.
- 한 단계 앞을 예측할 때는 단순히 주어진 과거 데이터를 입력값으로 사용하며 두 단계 앞을 예측할 때는 한 단계 예측값을 과거 데이터와 함께 입력으로 사용한다.
- 필요한 모든 예측값을 계산할 때까지 이 과정을 수행한다.

14.3.4 예측 구간

신경망 모델 \(y_{t}=f(\)y\(_{t-1})+\epsilon_{t}\)에서 오차는 정규분포를 따른다고 가정하기에 정규분포로부터 오차값을 무작위로 얻어 반복적으로 시뮬레이션할 수 있다.
- 예를 들어 \(T+1\)에서 \(\epsilon^{*}_{T+1}\)이 오차의 분포로부터 무작위로 뽑은 것이라고 하면, \(y^{*}_{T+1}=f(\)y\(_{T})+\epsilon^{*}_{T+1}\)로 \(y_{T+1}\)에 대한 추정값을 얻을 수 있다. 이 때, \(y^{*}_{T+1}\)은 \(y_{T+1}\)에 대한 예측분포로부터 뽑을 수 있는 하나의 가능한 값이다.

sim <- ts(matrix(0, nrow = 30L, 
                 ncol = 9L), 
          start = end(ridership.ts)[1L] + 1L) 


set.seed(10)
for(i in seq(9)){
  
  sim[,i] <- simulate(fit, nsim = 30L)

}

autoplot(ridership.ts) + 
  autolayer(sim) +
  ylab("Ridership")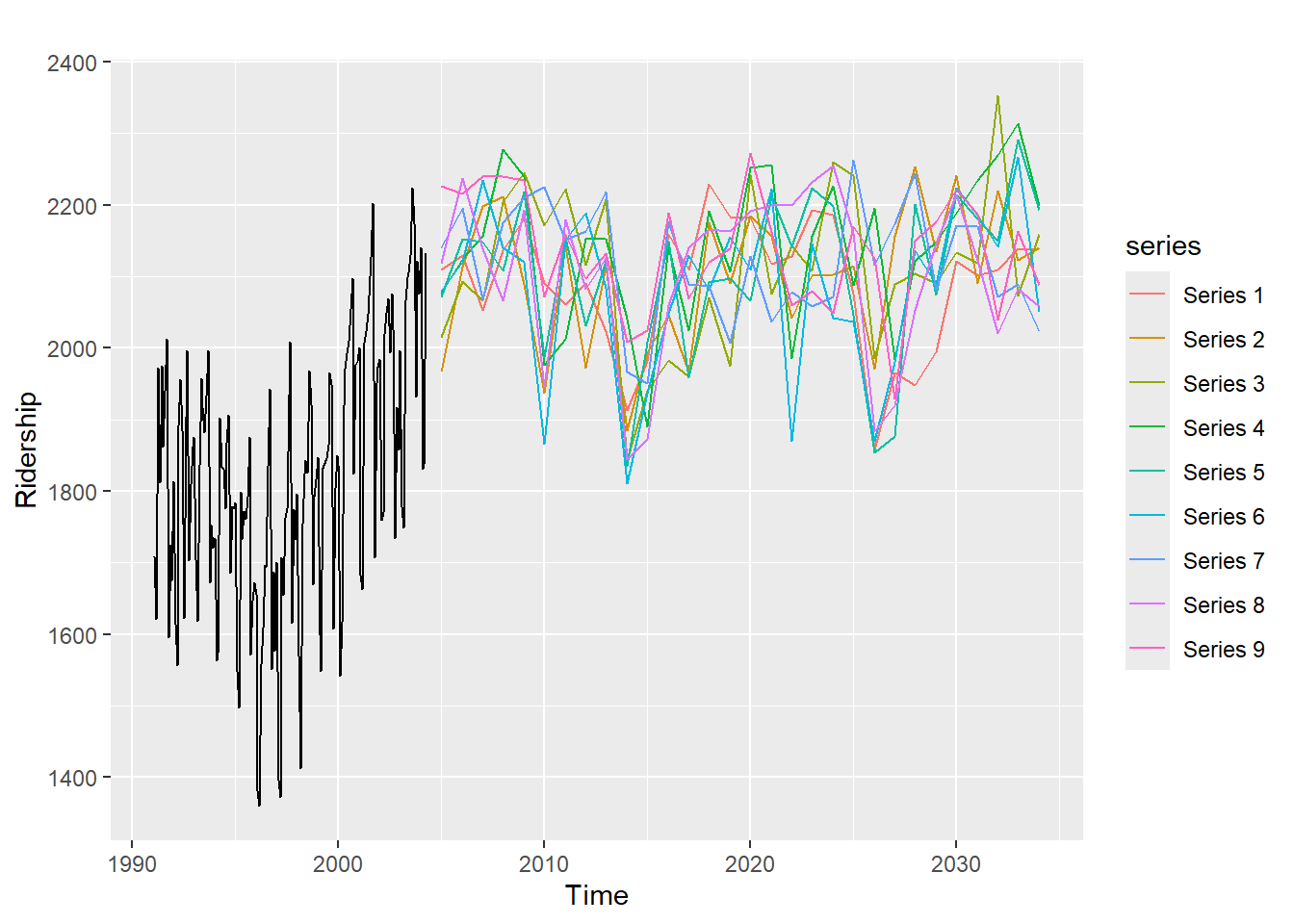

set.seed(10)
fcast <- forecast(fit,
                  PI = TRUE, 
                  npaths = 1000,                       # Npaths : How many simulation/ Normal error 
                  h = 30) 

autoplot(fcast) + 
  ylab("Ridership")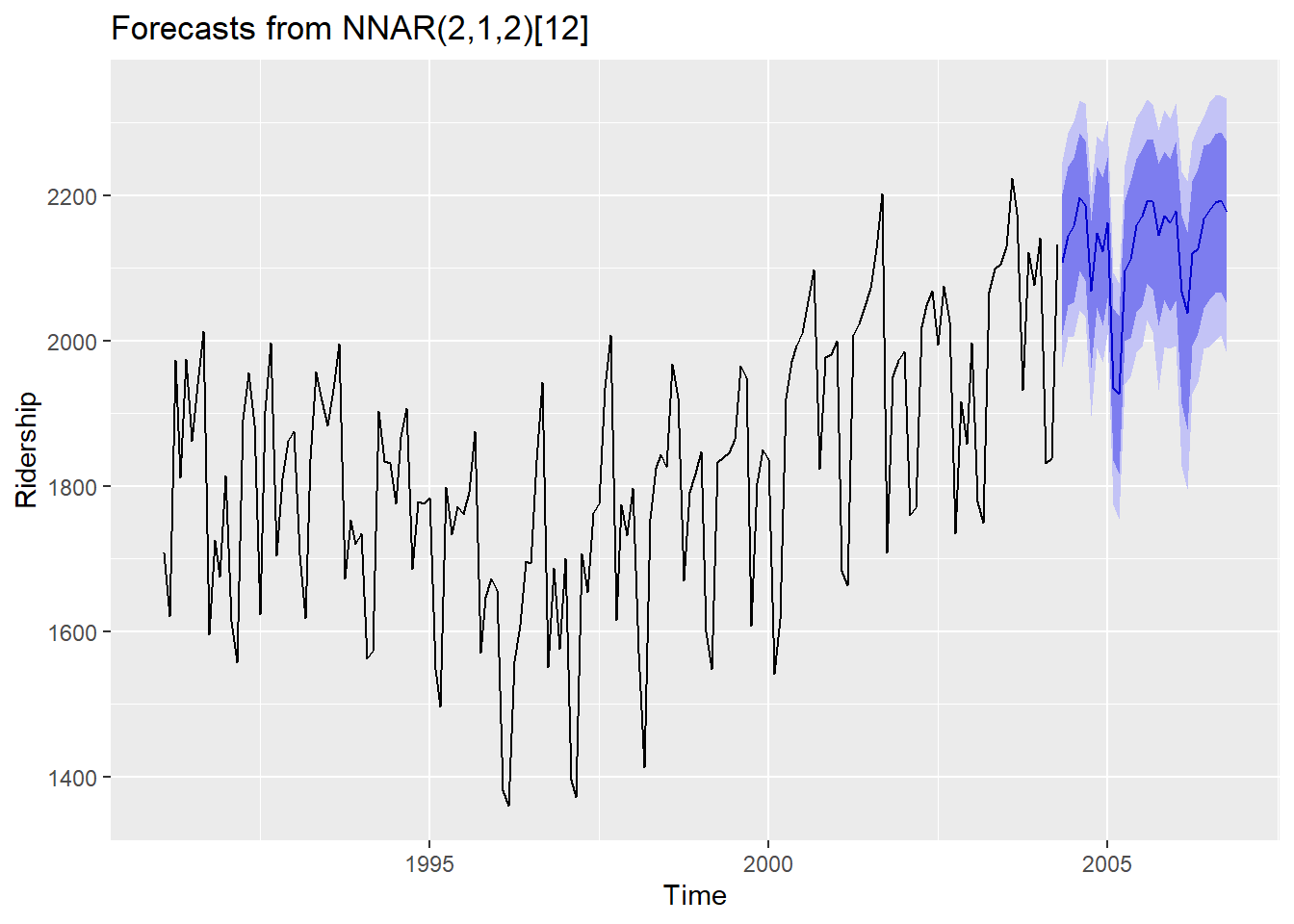

simulate 함수를 이용히여 예측구간을 구할 수도 있지만 forecast() 함수의 PI=TRUE를 통하여 예측구간을 얻을 수 있다.
- 오차는 기본적으로 정규분포에서 추출한다.