# 패키지 설치
pacman::p_load("evir")
# 데이터 불러오기
data(bmw, package = "evir")
# 시계열 그림
plot(bmw, type = "l")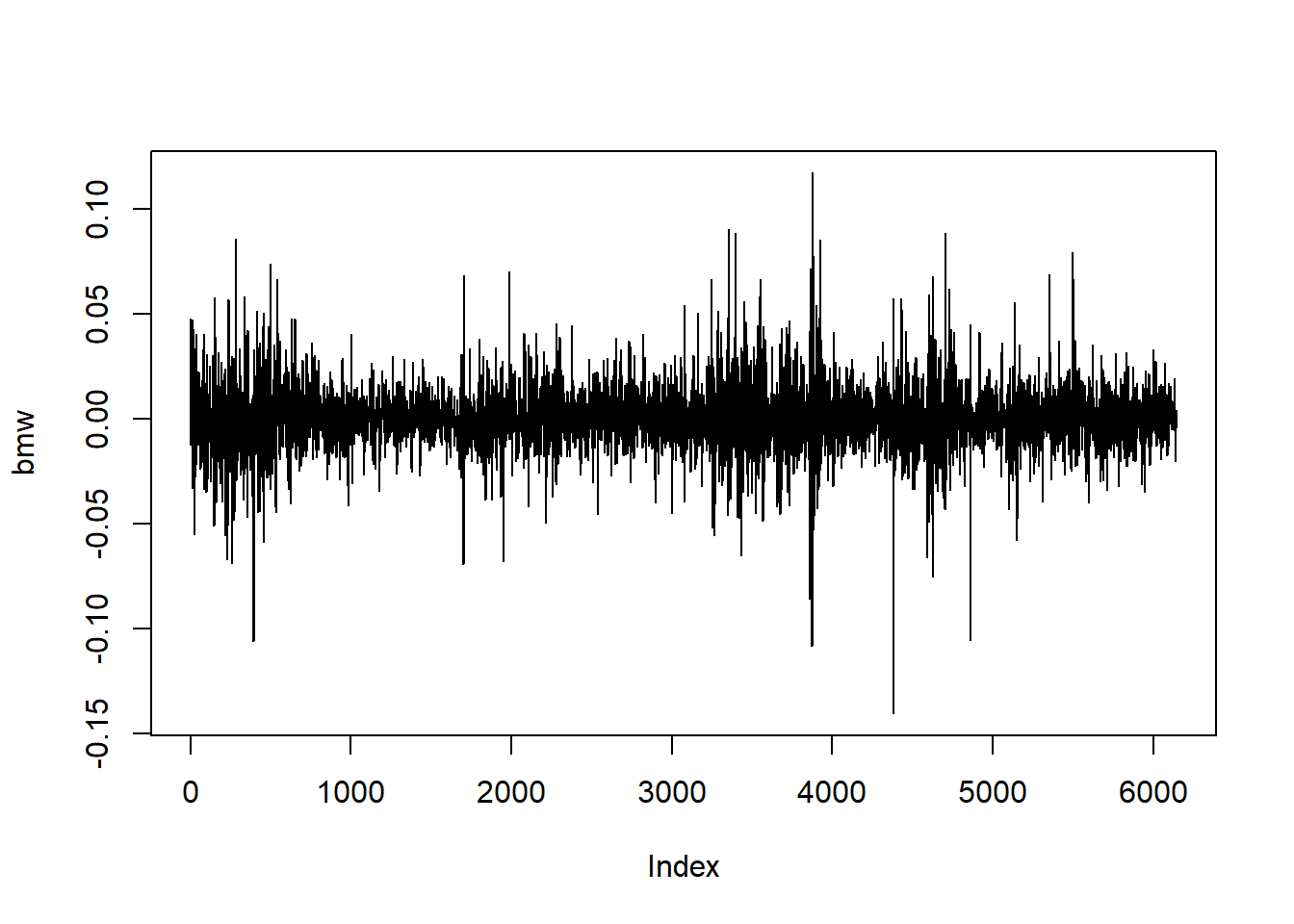
4 Autoregressive Moving Average Process
4.1 함수 설명
- 관측된 시계열에 자기회귀이동평균모형(Autoregressive Moving Average Model)을 구축하는 데 유용한 함수를 요약하면 다음과 같다.
| 함수 | 설명 |
|---|---|
arima() |
ARMA모형의 차수 \(p\)와 \(q\)를 지정하여 모형 구축 |
auto.arima() |
모형의 차수 지정없이 자동적으로 최적화된 모형 구축 |
acf() |
상관도표그림 |
pacf() |
부분상관도표그림 |
Box.test() |
Ljung-Box Test |
checkresiduals() |
잔차가 백색잡음과정의 가정을 만족하는지 확인할 때 사용 |
forecast() |
예측 |
4.2 예제
4.2.1 BMW 데이터셋
- Package
"evir"에서 제공하는 BMW 데이터셋은 1973년 1월부터 1996년 7월 사이에 BMW 주식의 일별 로그 수익률에 대한 시계열 데이터셋이다.
Result! 증가하거나 감소하는 추세가 없어서 시간의 흐름에 따라 평균이 일정하다.
# 상관도표그림
acf(bmw)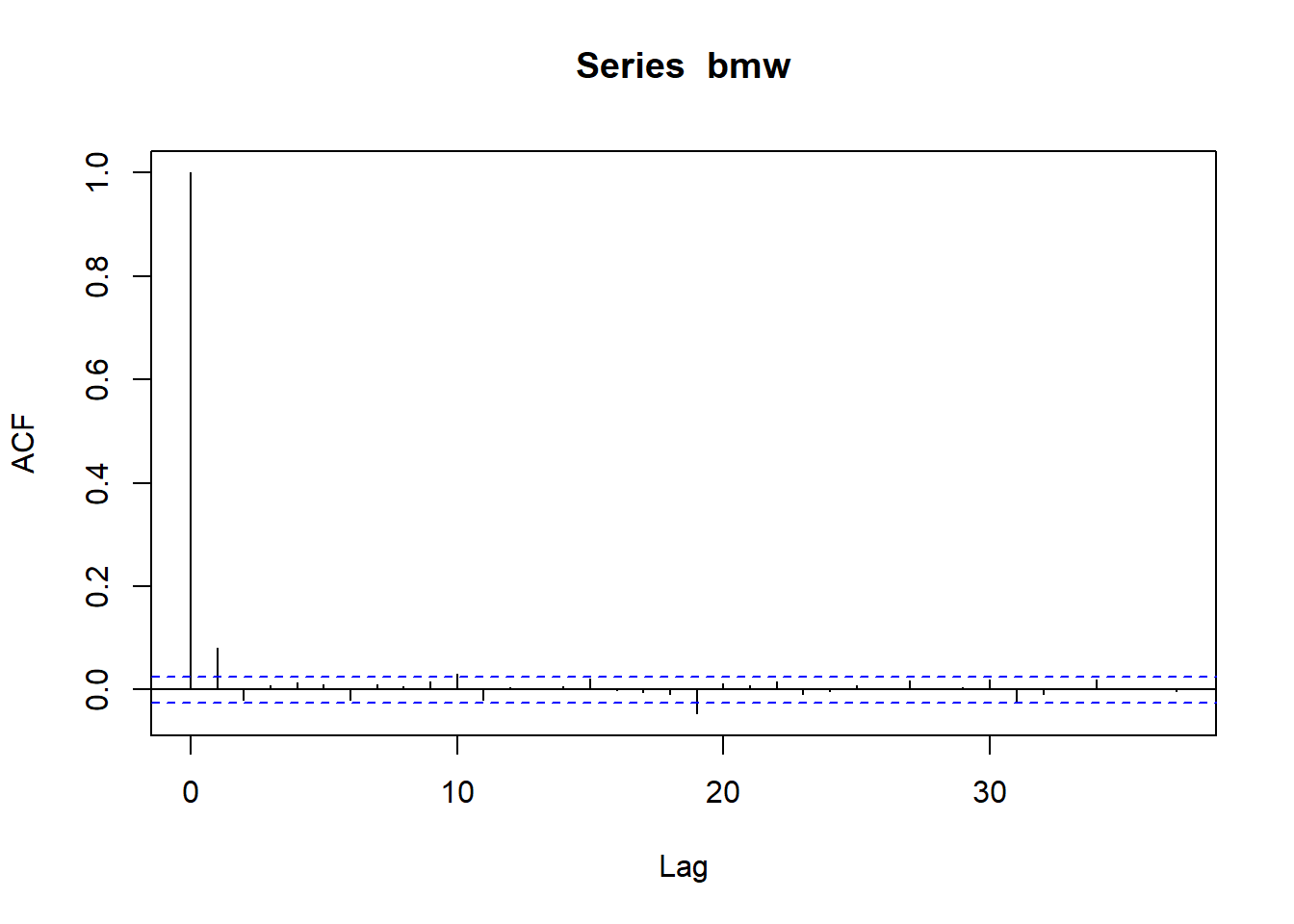
Result! 시차 1에서 막대의 끝이 파란색 선을 넘어가므로 시차 1에 대해 유의한 자기상관관계가 존재한다.
# 부분상관도표그림
pacf(bmw)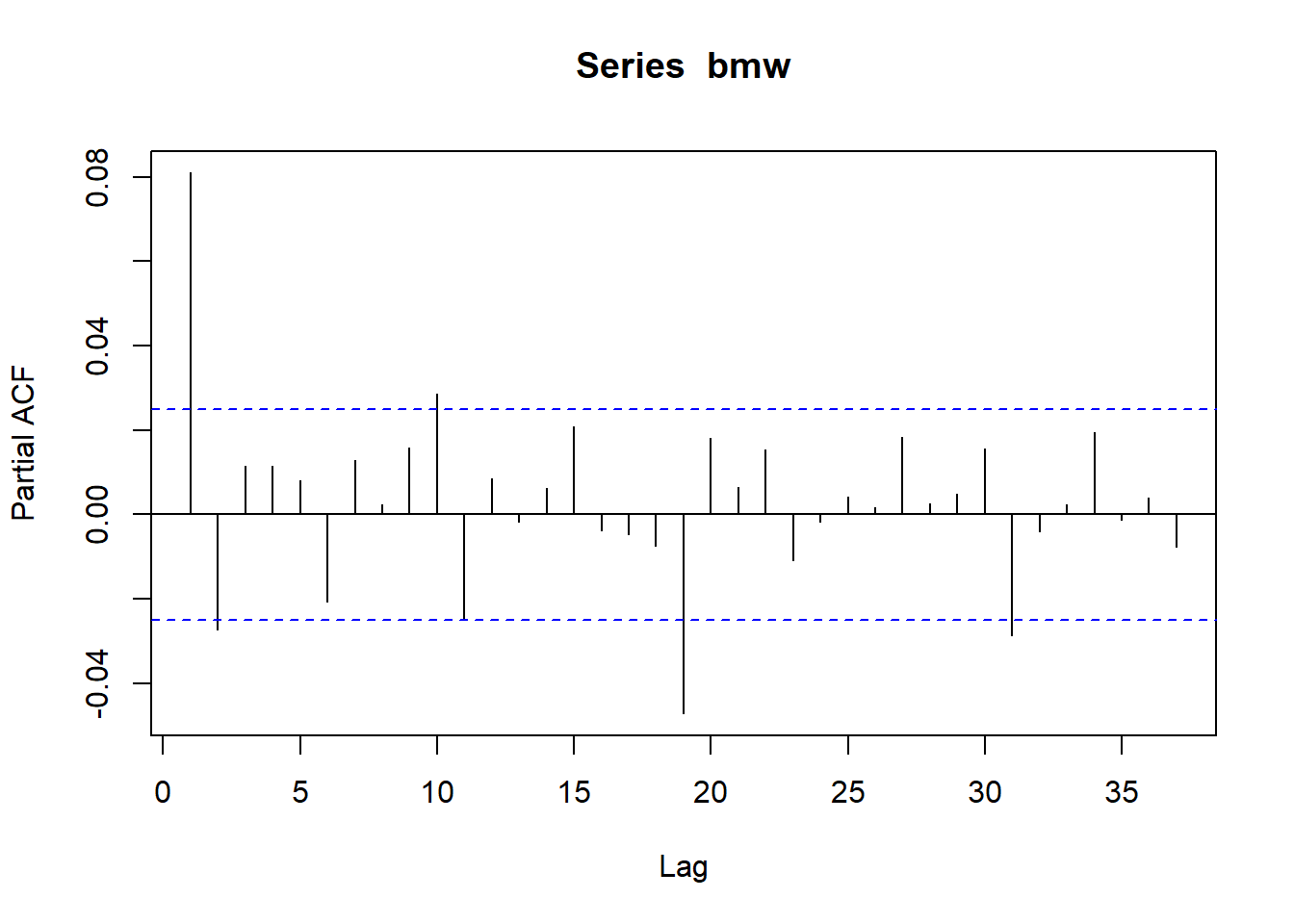
Result! 시차 1에서 막대의 끝이 파란색 선을 넘어가므로 시차 1에 대해 유의한 부분자기상관관계가 존재한다.
Caution! 큰 시차에서의 막대 끝이 파란색 선을 넘어가는 것은 우연 변동에 의한 가능성이 높다.
# Ljung-Box Test
Box.test(bmw, lag = 5,
type = "Ljung-Box")
Box-Ljung test
data: bmw
X-squared = 44.987, df = 5, p-value = 1.46e-08Result! 귀무가설 \(H_0 : \rho(1)=\rho(2)=\cdots=\rho(5)=0\)에 대한 검정 결과에 따르면, \(p\)값이 0에 가까우므로 유의수준 0.05에서 귀무가설을 기각한다. 즉, 관측된 시계열에 대해 \(\rho(1), \rho(2),\cdots,\rho(5)\) 중 유의한 자기상관관계가 적어도 1개 존재한다.
# Fit ARMA(1,1)
ARMA.bmw <- arima(bmw,
order = c(1, 0, 1)) Caution! 함수 arima()를 이용하여 ARMA(1,1) 모형을 구축하려면 옵션 order = c(1, 0, 1)을 입력한다. 만약, ARMA(\(p,q\)) 모형을 구축하려면 옵션 order = c(p, 0, q)을 입력하면 된다.
# 모형 추정 결과
print(ARMA.bmw)
Call:
arima(x = bmw, order = c(1, 0, 1))
Coefficients:
ar1 ma1 intercept
-0.2278 0.3122 4e-04
s.e. 0.1380 0.1349 2e-04
sigma^2 estimated as 0.0002161: log likelihood = 17214.87, aic = -34421.74Result! 출력 결과를 요약하면 다음과 같다.
1. 모수의 추정치는 \(\hat{\mu}=0.0004\), \(\hat{\phi}=-0.2278\), \(\hat{\theta}=0.3122\), \(\hat{\sigma}^2_\epsilon = 0.0002161\)이다. 이를 이용하면 관측된 시계열에 대해 구축된 ARMA(1,1) 모형은 \(Y_t-0.0004 = -0.2278(Y_{t-1}-0.0004)+ \epsilon_t + 0.3122\epsilon_{t-1}\)이다.
# 잔차를 이용한 백색잡음과정 체크
pacman::p_load("forecast")
checkresiduals(ARMA.bmw)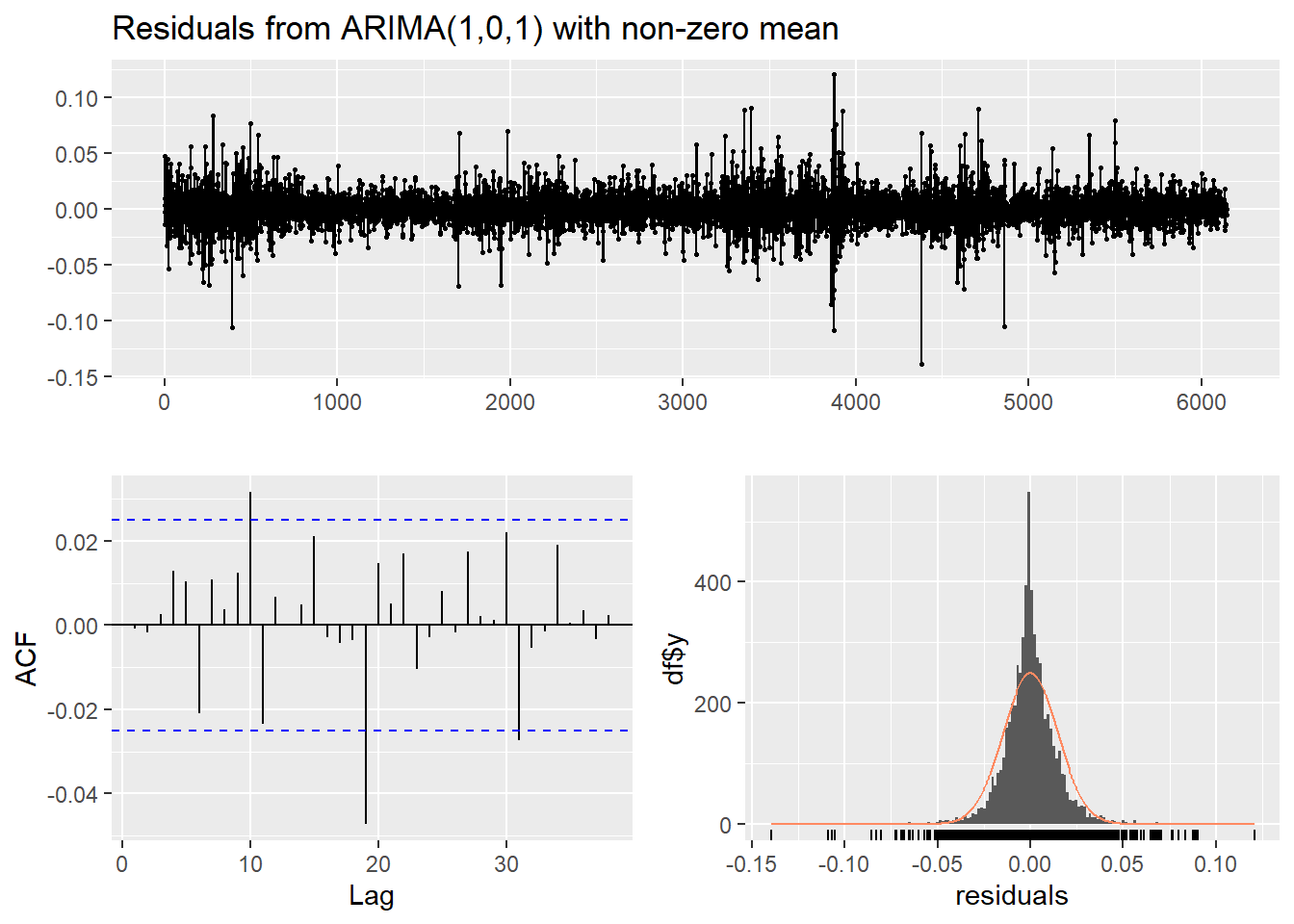
Ljung-Box test
data: Residuals from ARIMA(1,0,1) with non-zero mean
Q* = 12.394, df = 8, p-value = 0.1345
Model df: 2. Total lags used: 10Caution! Package "forecast"의 함수 checkresiduals()를 이용하여 잔차에 대한 모형 진단을 수행할 수 있다.
Result! 출력 그래프를 보면, 첫 번째 그래프는 잔차가 추세를 가지는지, 등분산성을 만족하는지 알 수 있다. ACF 그래프를 통해서는 잔차가 자기상관관계를 가지는지 알 수 있으며, 히스토그램을 통해 잔차가 좌우대칭 종 모양의 정규분포를 따르는지 알 수 있다.
“Ljung-Box” 검정 결과에 따르면, 귀무가설 \(H_0 : \rho(1)=\rho(2)=\cdots=\rho(10)=0\)에 대해 \(p\)값이 0.1345이므로 유의수준 0.05에서 \(p\)값이 0.05보다 크기 때문에 귀무가설을 기각하지 못한다. 즉, 잔차에 대해 시차 10까지의 자기상관계수 \(\rho(1), \rho(2), \cdots, \rho(10)\) 중 유의한 자기상관계수가 적어도 1개 존재한다는 증거가 부족하며, 해당 시계열에 대해 ARMA(1,1) 모형을 가정하는 것이 적절하다.
4.2.2 Mishkin 데이터
- Package
"Ecdat"에서 제공하는 Mishkin 데이터셋은 1950년 2월부터 1990년 12월 사이에 인플레이션율에 대한 시계열 데이터셋이다.
# 패키지 설치
pacman::p_load("Ecdat")
# 데이터 불러오기
data(Mishkin, package = "Ecdat")
y = as.vector(Mishkin[,1]) # 월별 인플레이션율 추출
y [1] -3.552289 5.247540 1.692860 5.064298 6.719322 11.668920 9.912501 8.346786 6.517766 4.865085 16.076321 19.154240 14.061910 4.650814 1.546310 4.627010 -1.540355 1.540355 0.000000
[20] 7.672257 6.102576 6.209472 4.533152 0.000000 -7.564866 0.000000 19.570490 -1.494151 1.494151 0.000000 -1.494151 0.000000 1.494151 0.000000 -1.494151 -2.993894 -6.010291 3.008908
[39] 1.501630 2.997634 4.482457 2.979029 2.971549 1.483071 2.960655 -4.443726 -1.484906 2.967978 -1.483071 -1.484906 -2.839906 2.839906 1.484906 0.000000 -1.484906 -2.839906 -2.982291
[58] 2.982291 -2.982291 0.000000 0.000000 1.492020 0.000000 0.000000 0.000000 2.978693 -2.978693 4.330177 0.000000 1.484906 -2.836390 0.000000 0.000000 2.836390 1.483071 5.914023
[77] 5.751562 8.774637 -1.457907 1.457907 5.682521 1.449363 2.893485 0.000000 2.886525 2.748830 2.873018 2.866156 7.006195 5.678584 1.415482 1.413814 0.000000 4.103441 0.000000
[96] 7.020216 1.399128 6.844860 2.777502 0.000000 1.386248 1.384744 0.000000 0.000000 1.383148 1.381556 -1.381556 1.381556 -1.381556 0.000000 1.381556 1.254555 5.504627 2.742874
[115] -1.370653 2.739743 3.973921 1.363010 -2.727571 1.364560 0.000000 6.799529 0.000000 2.586158 0.000000 0.000000 1.352397 5.394306 1.344819 0.000000 0.000000 1.343314 -1.343314
[134] 1.343314 0.000000 1.341812 5.230890 -1.335972 2.670459 0.000000 0.000000 0.000000 0.000000 2.664529 2.658626 2.532271 0.000000 0.000000 2.647071 0.000000 6.592472 -1.315600
[153] 0.000000 -1.317044 1.317044 1.315600 1.194725 0.000000 0.000000 5.242814 3.917133 0.000000 1.302875 1.183181 0.000000 2.598952 0.000000 0.000000 -1.298772 1.298772 2.593336
[172] 0.000000 2.587653 1.291782 -1.291782 2.582175 1.171857 2.574118 1.284992 -1.284992 0.000000 1.284992 3.846739 2.557659 6.254851 1.270154 -2.541654 2.541654 0.000000 2.536194
[191] 3.679570 0.000000 7.553715 2.393494 4.999561 0.000000 2.491991 2.486741 7.317456 1.233940 4.811423 0.000000 0.000000 0.000000 1.227743 2.451723 2.446724 3.549967 3.649961
[210] 4.849325 2.307577 3.617287 3.606416 2.289339 3.588767 4.768305 3.456034 4.735883 3.539687 4.596686 3.515803 3.399432 3.495549 3.485477 5.681739 3.458990 2.300467 3.338259
[229] 4.574945 6.726781 5.662605 3.282331 7.861482 3.252032 4.457231 4.339972 4.424734 5.408054 7.570396 2.182552 5.439077 3.153226 7.553640 4.197689 3.211568 5.236804 2.126986
[248] 4.242622 6.240278 4.110415 5.237093 2.088382 5.110830 5.183215 6.096802 5.041712 6.133401 2.962434 1.016681 1.015820 2.029064 1.013247 3.952596 1.009064 5.945445 3.007194
[267] 2.999539 2.901685 2.984980 2.977574 2.880218 4.934430 2.950948 3.834231 2.934329 5.758887 8.630559 11.440700 9.436906 6.536329 7.438794 3.659775 19.304211 1.838323 7.242186
[286] 8.105994 8.051480 9.785962 15.814170 12.122030 6.883693 12.010690 10.111450 7.566704 13.394280 12.342670 9.006326 9.680984 7.246837 4.855838 6.371189 4.738003 4.719480 5.566699
[305] 9.340268 12.388900 4.665991 5.350513 6.864336 6.061113 5.269925 3.040442 3.720887 3.778037 5.200997 6.673568 7.379198 5.857414 5.093520 5.072093 5.117023 3.575525 5.014266
[324] 6.435108 12.054450 6.336976 9.123064 6.255971 7.616233 4.105433 4.782352 2.760079 4.065748 5.420399 4.033883 6.056223 7.374409 8.668254 9.873637 10.451070 11.012750 5.793180
[343] 5.119508 7.025764 7.623123 6.306279 6.273224 9.946648 11.106510 10.389710 11.519510 13.766670 11.877010 9.987637 9.318593 10.410780 9.167216 6.281625 9.620259 14.005740 14.956960
[362] 14.772750 8.707769 10.170030 8.572340 7.396264 9.999892 11.967070 7.265405 7.174647 7.693233 10.614180 15.060890 9.936591 6.880011 7.334265 6.843737 9.197388 8.644333 9.498251
[381] 5.220479 4.722268 4.229963 6.531282 3.765132 1.835451 1.875277 8.318006 11.909480 8.179443 2.243804 5.880264 5.358331 1.808168 0.903063 2.664138 0.409372 0.818200 8.558391
[400] 6.479959 4.032262 4.820824 4.002672 5.979086 3.176779 1.981179 1.582568 6.702875 5.491976 2.736532 5.843219 3.492417 3.868475 3.856044 4.994358 5.737063 3.048542 0.000000
[419] 0.760985 2.279948 4.924980 5.281344 4.883469 4.490115 3.729027 1.860177 2.599458 3.703707 3.692311 4.048485 2.935736 3.659655 -3.293165 -5.508809 -2.579503 3.683244 5.869799
[438] 0.365932 2.193139 5.828813 1.089709 1.088720 1.087844 7.226761 4.308729 5.364409 6.405601 4.251591 4.236581 3.167622 6.310269 6.277260 3.126359 1.040348 0.000000 3.115431
[457] 3.107574 5.161263 6.164397 4.092111 5.095515 5.073969 5.052708 8.040197 3.999936 0.998057 1.993322 5.960278 4.944349 6.888122 7.823956 6.804426 2.904398 2.897386 1.927679
[476] 3.846190 5.746220 2.862824 1.904730 12.307830 5.638225 6.544558 1.863323 2.789618 6.484031 4.610040 10.992540 9.988676 7.212614 2.693695 0.000000# 시계열 그림
plot(y, type = "l")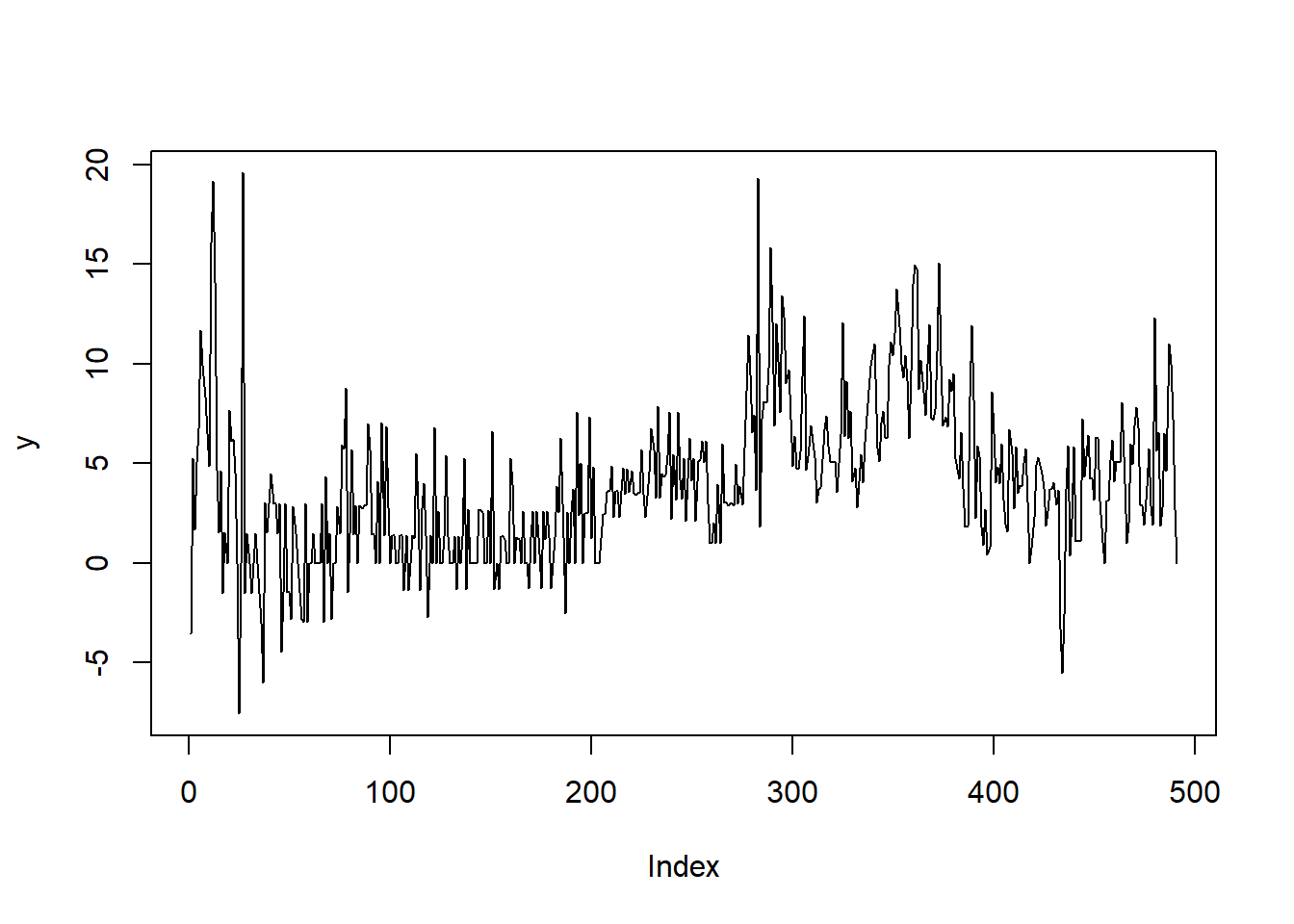
# 상관도표그림
acf(y)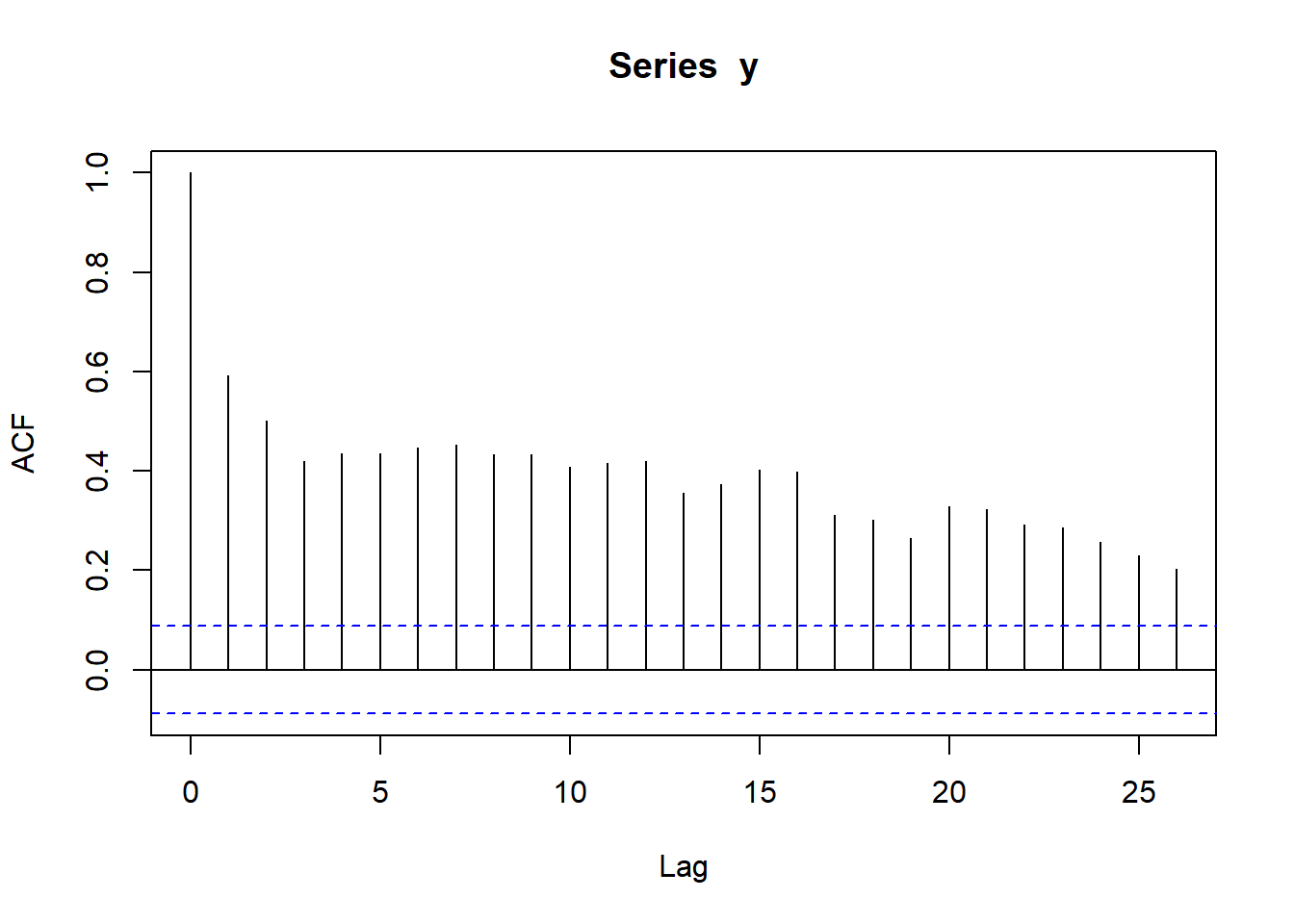
Result! 대부분의 시차에서 막대의 끝이 파란색 선을 넘어가므로 시차 25까지 유의한 자기상관관계가 존재한다.
# 부분상관도표그림
pacf(y)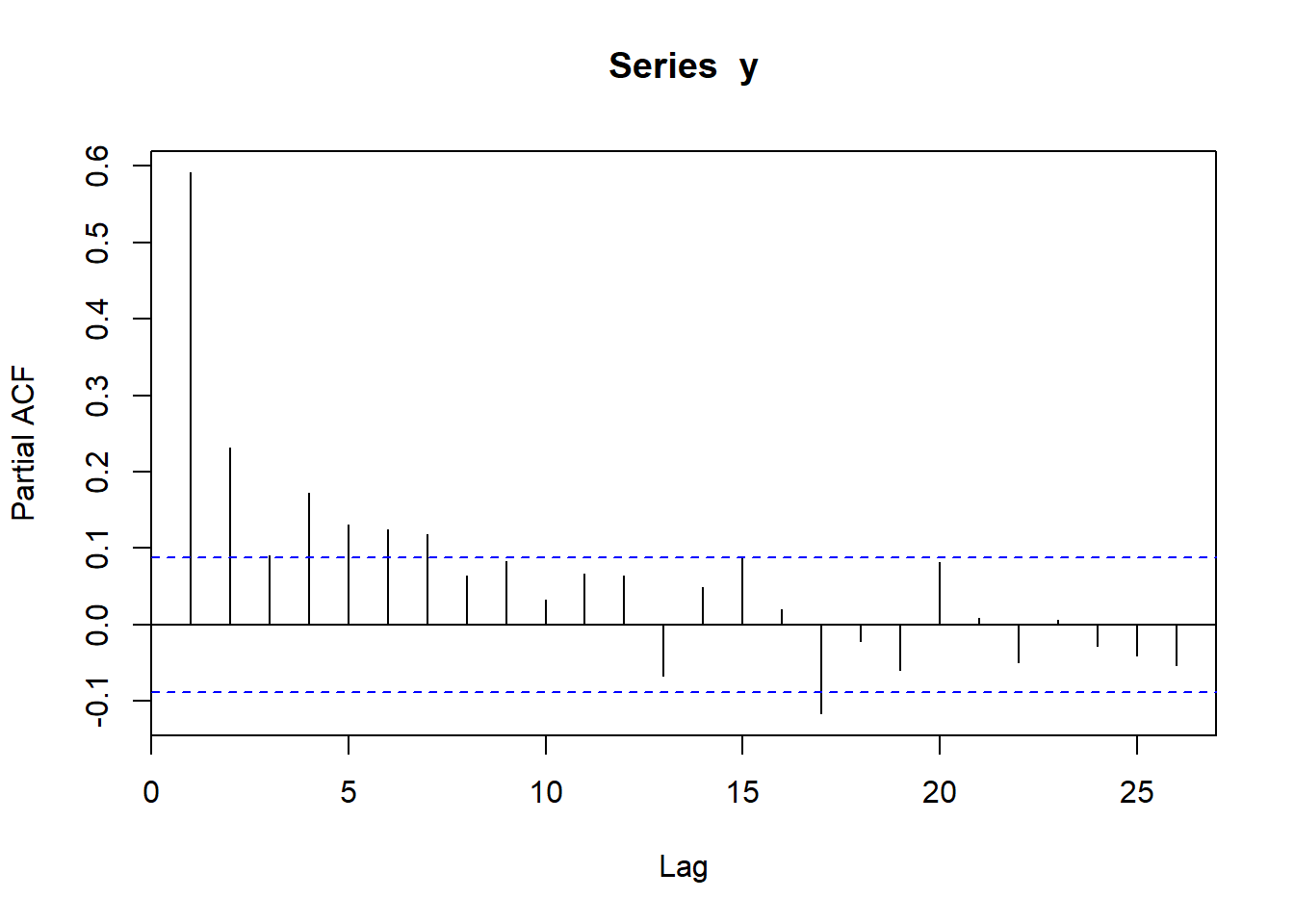
Result! 시차 7까지 막대의 끝이 파란색 선을 넘어가므로 시차 7까지 유의한 부분자기상관관계가 존재한다.
# Ljung-Box Test
Box.test(y, lag = 7,
type = "Ljung-Box")
Box-Ljung test
data: y
X-squared = 774.34, df = 7, p-value < 2.2e-16Result! 귀무가설 \(H_0 : \rho(1)=\rho(2)=\cdots=\rho(7)=0\)에 대한 검정 결과에 따르면, \(p\)값이 0에 가까우므로 유의수준 0.05에서 귀무가설을 기각한다. 즉, 관측된 시계열에 대해 \(\rho(1), \rho(2),\cdots,\rho(7)\) 중 유의한 자기상관관계가 적어도 1개 존재한다.
# Fit ARMA(1,1)
ARMA.y <- arima(y,
order = c(1, 0, 1))
# 잔차를 이용한 백색잡음과정 체크
checkresiduals(ARMA.y)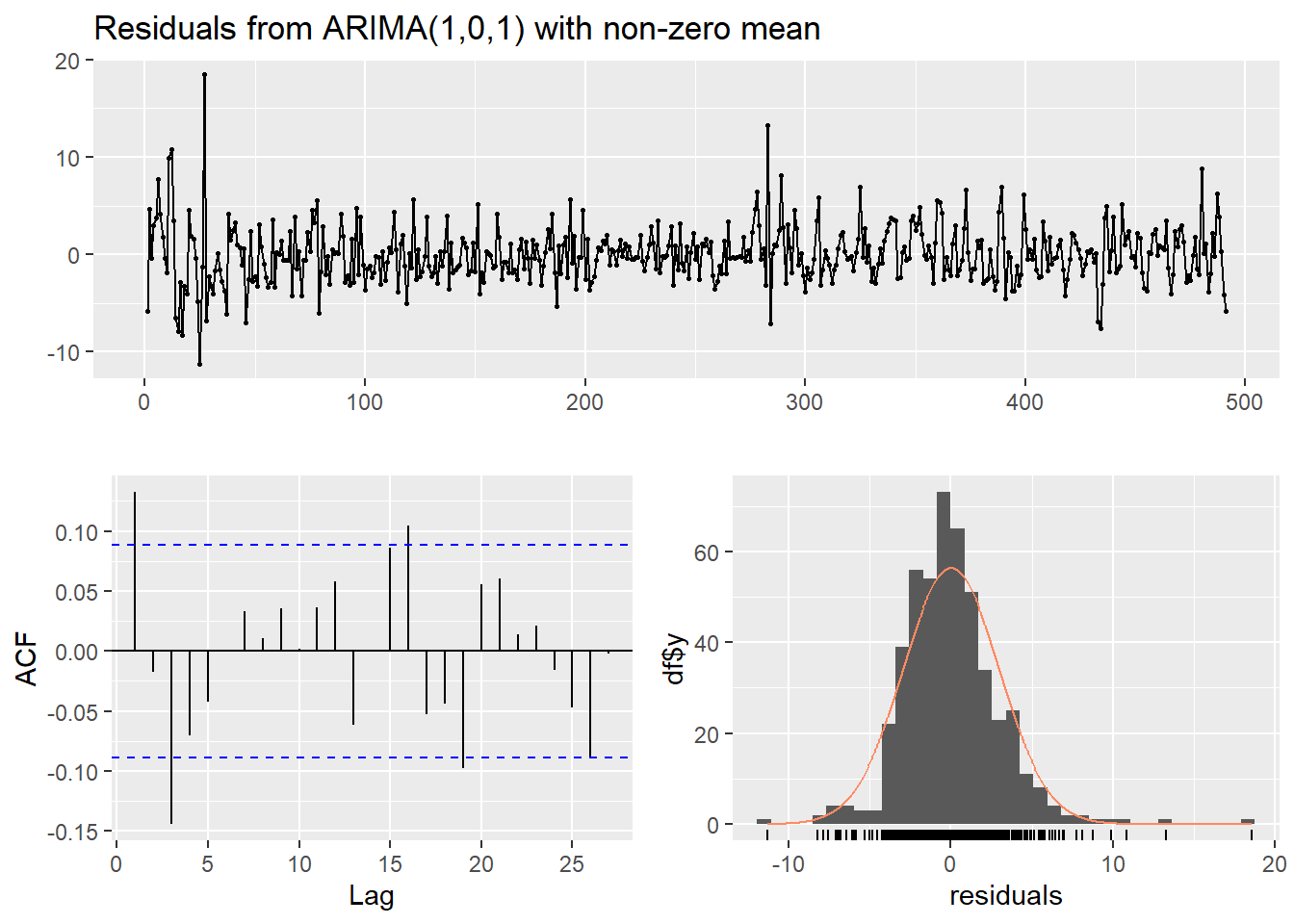
Ljung-Box test
data: Residuals from ARIMA(1,0,1) with non-zero mean
Q* = 23.724, df = 8, p-value = 0.002549
Model df: 2. Total lags used: 10Result! ACF 그래프를 보면 시차 2에서 막대의 끝이 파란색 선을 넘어가므로 자기상관계수가 통계적으로 유의하다. 즉, 시차 2의 잔차들은 유의한 자기상관계수를 가지므로 백색잡음과정의 독립성 가정을 만족하지 않는다.
게다가, “Ljung-Box” 검정 결과에 따르면, 귀무가설 \(H_0 : \rho(1)=\rho(2)=\cdots=\rho(10)=0\)에 대해 \(p\)값이 0.002549이므로 유의수준 0.05에서 \(p\)값이 0.05보다 작아 귀무가설을 기각한다. 즉, 잔차에 대해 시차 10까지의 자기상관계수 \(\rho(1), \rho(2), \cdots, \rho(10)\) 중 유의한 자기상관계수가 적어도 1개 존재한다는 것을 의미하며, 해당 시계열에 대해 ARMA(1,1) 모형을 가정하는 것은 적절하지 않다.
Caution! Package "forecast"에서 제공하는 함수 auto.arima()에 옵션 max.p = 20, max.q = 20, d = 0을 입력하여 최적의 ARMA(\(p,q\)) 모형을 찾을 수 있다.
pacman::p_load("forecast")
auto.y2 <- auto.arima(y, max.p = 20,
max.q = 20, d = 0,
ic = "aic") # AIC 기준으로 AIC가 가장 작은 모형을 최적 모형으로 선택
print(auto.y2)Series: y
ARIMA(2,0,1) with non-zero mean
Coefficients:
ar1 ar2 ma1 mean
1.2074 -0.2237 -0.8573 4.1068
s.e. 0.0587 0.0551 0.0337 1.0692
sigma^2 = 8.533: log likelihood = -1221.52
AIC=2453.03 AICc=2453.16 BIC=2474.02Result! 관측된 시계열에 대해 AIC를 기준으로 최적의 모형은 ARMA(2,1) 모형이다. 모수 추정 결과에 따르면, \(\hat{\mu} = 4.1068\), \(\hat{\phi}_1=1.2074\), \(\hat{\phi}_2=-0.2237\), \(\hat{\theta}=-0.8573\), \(\hat{\sigma}^2_\epsilon = 8.533\)이다. 이를 이용하면 관측된 시계열에 대해 구축된 ARMA(2,1) 모형은 \(Y_t-4.1068 = 1.2074(Y_{t-1}-4.1068)-0.2237(Y_{t-2}-4.1068)+\epsilon_t -0.8573\epsilon_{t-1}\)이다.
# 잔차를 이용한 백색잡음과정 체크
checkresiduals(auto.y2)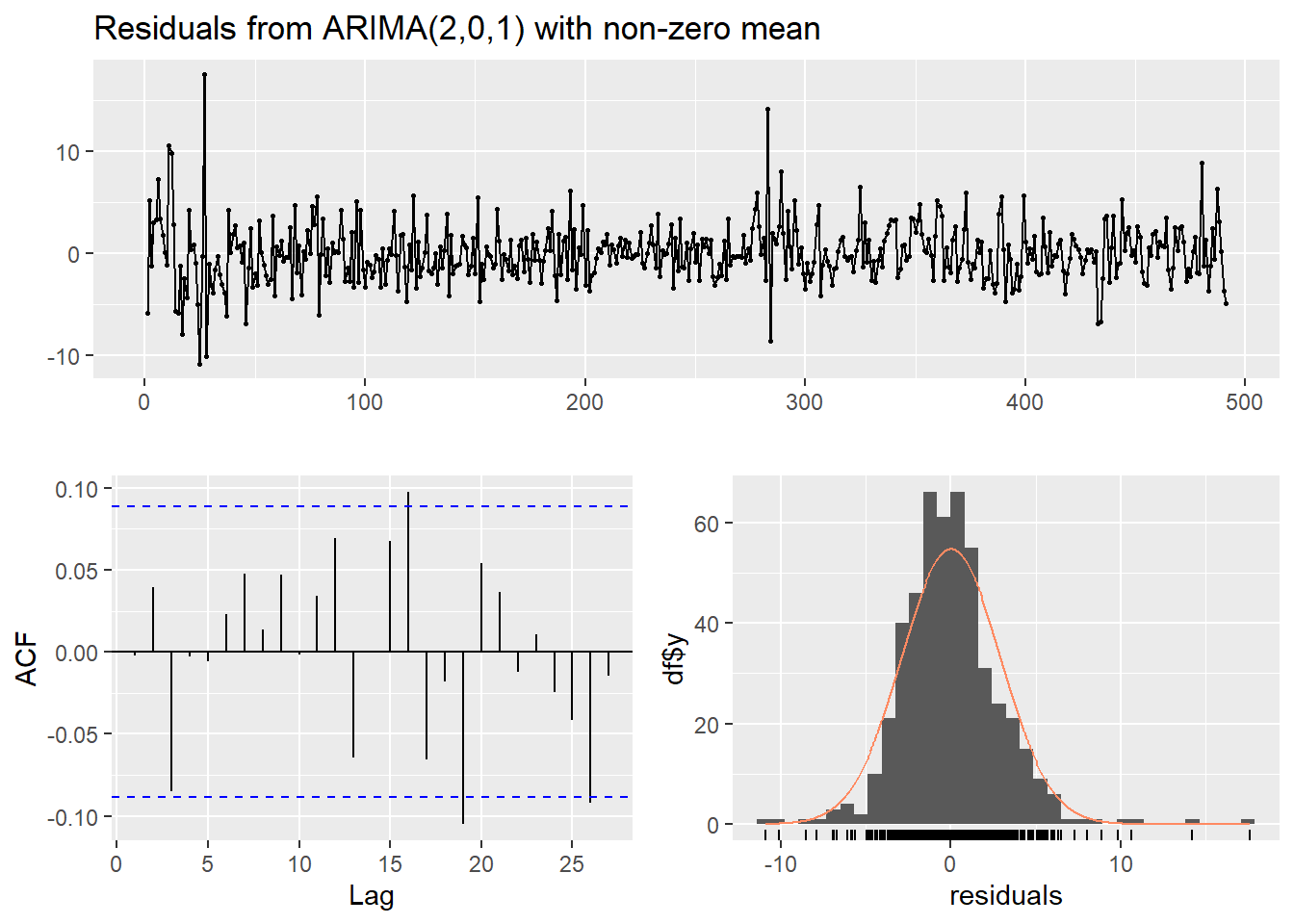
Ljung-Box test
data: Residuals from ARIMA(2,0,1) with non-zero mean
Q* = 6.9828, df = 7, p-value = 0.4307
Model df: 3. Total lags used: 10Result! 히스토그램을 살펴보면, 왼쪽으로 치우친 그래프 모양임을 알 수 있다.
게다가, “Ljung-Box” 검정 결과에 따르면, 귀무가설 \(H_0 : \rho(1)=\rho(2)=\cdots=\rho(10)=0\)에 대해 \(p\)값이 0.4307이므로 유의수준 0.05에서 \(p\)값이 0.05보다 크기 때문에 귀무가설을 기각하지 못한다. 즉, 잔차에 대해 시차 10까지의 자기상관계수 \(\rho(1), \rho(2), \cdots, \rho(10)\) 중 유의한 자기상관계수가 적어도 1개 존재한다는 증거가 부족하며, 해당 시계열에 대해 ARMA(2,1) 모형을 가정하는 것이 적절하다.