pacman::p_load("data.table",
"tidyverse",
"dplyr", "tidyr",
"ggplot2", "GGally",
"caret",
"rpart", # For Decision Tree
"rattle", "rpart.plot", # For fancyRpartPlot
"visNetwork", "sparkline") # For visTree
titanic <- fread("../Titanic.csv") # 데이터 불러오기
titanic %>%
as_tibble3 Decision Tree
Tree-based Algorithm
- 범주형 예측 변수와 연속형 예측 변수 모두 적용이 가능하다.
- 예측 변수에 대한 분포 가정이 필요없다.
- 다른 척도를 가지는 연속형 예측 변수들에 대해 별도의 변환과정 없이 적용가능하다.
- 표준화/정규화 수행 X
실습 자료 : 1912년 4월 15일 타이타닉호 침몰 당시 탑승객들의 정보를 기록한 데이터셋이며, 총 11개의 변수를 포함하고 있다. 이 자료에서 Target은
Survived이다.
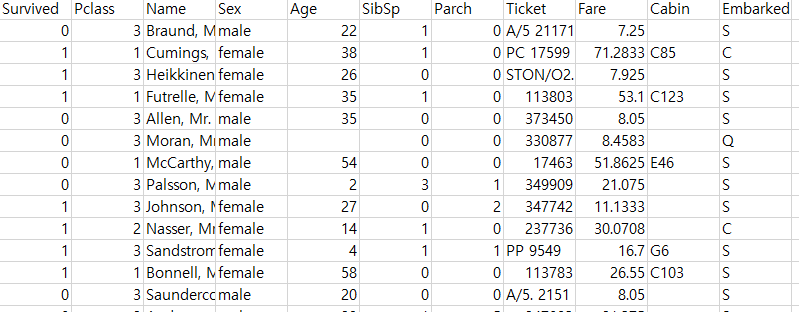

3.1 데이터 불러오기
# A tibble: 891 × 11
Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
<int> <int> <chr> <chr> <dbl> <int> <int> <chr> <dbl> <chr> <chr>
1 0 3 Braund, Mr. Owen Harris male 22 1 0 A/5 21171 7.25 "" S
2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Thayer) female 38 1 0 PC 17599 71.3 "C85" C
3 1 3 Heikkinen, Miss. Laina female 26 0 0 STON/O2. 3101282 7.92 "" S
4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35 1 0 113803 53.1 "C123" S
5 0 3 Allen, Mr. William Henry male 35 0 0 373450 8.05 "" S
6 0 3 Moran, Mr. James male NA 0 0 330877 8.46 "" Q
7 0 1 McCarthy, Mr. Timothy J male 54 0 0 17463 51.9 "E46" S
8 0 3 Palsson, Master. Gosta Leonard male 2 3 1 349909 21.1 "" S
9 1 3 Johnson, Mrs. Oscar W (Elisabeth Vilhelmina Berg) female 27 0 2 347742 11.1 "" S
10 1 2 Nasser, Mrs. Nicholas (Adele Achem) female 14 1 0 237736 30.1 "" C
# ℹ 881 more rows3.2 데이터 전처리 I
titanic %<>%
data.frame() %>% # Data Frame 형태로 변환
mutate(Survived = ifelse(Survived == 1, "yes", "no")) # Target을 문자형 변수로 변환
# 1. Convert to Factor
fac.col <- c("Pclass", "Sex",
# Target
"Survived")
titanic <- titanic %>%
mutate_at(fac.col, as.factor) # 범주형으로 변환
glimpse(titanic) # 데이터 구조 확인Rows: 891
Columns: 11
$ Survived <fct> no, yes, yes, yes, no, no, no, no, yes, yes, yes, yes, no, no, no, yes, no, yes, no, yes, no, yes, yes, yes, no, yes, no, no, yes, no, no, yes, yes, no, no, no, yes, no, no, yes, no…
$ Pclass <fct> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3, 2, 3, 3, 2, 2, 3, 1, 3, 3, 3, 1, 3, 3, 1, 1, 3, 2, 1, 1, 3, 3, 3, 3, 3, 2, 3, 2, 3, 3, 3, 3, 3, 3, 3, 3, 1, 2, 1, 1, 2, 3, 2, 3, 3…
$ Name <chr> "Braund, Mr. Owen Harris", "Cumings, Mrs. John Bradley (Florence Briggs Thayer)", "Heikkinen, Miss. Laina", "Futrelle, Mrs. Jacques Heath (Lily May Peel)", "Allen, Mr. William Henry…
$ Sex <fct> male, female, female, female, male, male, male, male, female, female, female, female, male, male, female, female, male, male, female, female, male, male, female, male, female, femal…
$ Age <dbl> 22.0, 38.0, 26.0, 35.0, 35.0, NA, 54.0, 2.0, 27.0, 14.0, 4.0, 58.0, 20.0, 39.0, 14.0, 55.0, 2.0, NA, 31.0, NA, 35.0, 34.0, 15.0, 28.0, 8.0, 38.0, NA, 19.0, NA, NA, 40.0, NA, NA, 66.…
$ SibSp <int> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1, 1, 0, 0, 1, 0, 0, 4, 0, 1, 0, 0, 0, 0, 0, 3, 1, 0, 3, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 2, 1, 1, 1, 0, 1, 0, 0, 1, 0, 2, 1, 4, 0, 1, 1, 0, 0, 0, 0, 1, 5, 0…
$ Parch <int> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 5, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 5, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 2, 2, 0…
$ Ticket <chr> "A/5 21171", "PC 17599", "STON/O2. 3101282", "113803", "373450", "330877", "17463", "349909", "347742", "237736", "PP 9549", "113783", "A/5. 2151", "347082", "350406", "248706", "38…
$ Fare <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, 51.8625, 21.0750, 11.1333, 30.0708, 16.7000, 26.5500, 8.0500, 31.2750, 7.8542, 16.0000, 29.1250, 13.0000, 18.0000, 7.2250, 26.0000,…
$ Cabin <chr> "", "C85", "", "C123", "", "", "E46", "", "", "", "G6", "C103", "", "", "", "", "", "", "", "", "", "D56", "", "A6", "", "", "", "C23 C25 C27", "", "", "", "B78", "", "", "", "", ""…
$ Embarked <chr> "S", "C", "S", "S", "S", "Q", "S", "S", "S", "C", "S", "S", "S", "S", "S", "S", "Q", "S", "S", "C", "S", "S", "Q", "S", "S", "S", "C", "S", "Q", "S", "C", "C", "Q", "S", "C", "S", "…# 2. Generate New Variable
titanic <- titanic %>%
mutate(FamSize = SibSp + Parch) # "FamSize = 형제 및 배우자 수 + 부모님 및 자녀 수"로 가족 수를 의미하는 새로운 변수
glimpse(titanic) # 데이터 구조 확인Rows: 891
Columns: 12
$ Survived <fct> no, yes, yes, yes, no, no, no, no, yes, yes, yes, yes, no, no, no, yes, no, yes, no, yes, no, yes, yes, yes, no, yes, no, no, yes, no, no, yes, yes, no, no, no, yes, no, no, yes, no…
$ Pclass <fct> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3, 2, 3, 3, 2, 2, 3, 1, 3, 3, 3, 1, 3, 3, 1, 1, 3, 2, 1, 1, 3, 3, 3, 3, 3, 2, 3, 2, 3, 3, 3, 3, 3, 3, 3, 3, 1, 2, 1, 1, 2, 3, 2, 3, 3…
$ Name <chr> "Braund, Mr. Owen Harris", "Cumings, Mrs. John Bradley (Florence Briggs Thayer)", "Heikkinen, Miss. Laina", "Futrelle, Mrs. Jacques Heath (Lily May Peel)", "Allen, Mr. William Henry…
$ Sex <fct> male, female, female, female, male, male, male, male, female, female, female, female, male, male, female, female, male, male, female, female, male, male, female, male, female, femal…
$ Age <dbl> 22.0, 38.0, 26.0, 35.0, 35.0, NA, 54.0, 2.0, 27.0, 14.0, 4.0, 58.0, 20.0, 39.0, 14.0, 55.0, 2.0, NA, 31.0, NA, 35.0, 34.0, 15.0, 28.0, 8.0, 38.0, NA, 19.0, NA, NA, 40.0, NA, NA, 66.…
$ SibSp <int> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1, 1, 0, 0, 1, 0, 0, 4, 0, 1, 0, 0, 0, 0, 0, 3, 1, 0, 3, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 2, 1, 1, 1, 0, 1, 0, 0, 1, 0, 2, 1, 4, 0, 1, 1, 0, 0, 0, 0, 1, 5, 0…
$ Parch <int> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 5, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 5, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 2, 2, 0…
$ Ticket <chr> "A/5 21171", "PC 17599", "STON/O2. 3101282", "113803", "373450", "330877", "17463", "349909", "347742", "237736", "PP 9549", "113783", "A/5. 2151", "347082", "350406", "248706", "38…
$ Fare <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, 51.8625, 21.0750, 11.1333, 30.0708, 16.7000, 26.5500, 8.0500, 31.2750, 7.8542, 16.0000, 29.1250, 13.0000, 18.0000, 7.2250, 26.0000,…
$ Cabin <chr> "", "C85", "", "C123", "", "", "E46", "", "", "", "G6", "C103", "", "", "", "", "", "", "", "", "", "D56", "", "A6", "", "", "", "C23 C25 C27", "", "", "", "B78", "", "", "", "", ""…
$ Embarked <chr> "S", "C", "S", "S", "S", "Q", "S", "S", "S", "C", "S", "S", "S", "S", "S", "S", "Q", "S", "S", "C", "S", "S", "Q", "S", "S", "S", "C", "S", "Q", "S", "C", "C", "Q", "S", "C", "S", "…
$ FamSize <int> 1, 1, 0, 1, 0, 0, 0, 4, 2, 1, 2, 0, 0, 6, 0, 0, 5, 0, 1, 0, 0, 0, 0, 0, 4, 6, 0, 5, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 2, 1, 1, 1, 0, 3, 0, 0, 1, 0, 2, 1, 5, 0, 1, 1, 1, 0, 0, 0, 3, 7, 0…# 3. Select Variables used for Analysis
titanic1 <- titanic %>%
select(Survived, Pclass, Sex, Age, Fare, FamSize) # 분석에 사용할 변수 선택
glimpse(titanic1) # 데이터 구조 확인Rows: 891
Columns: 6
$ Survived <fct> no, yes, yes, yes, no, no, no, no, yes, yes, yes, yes, no, no, no, yes, no, yes, no, yes, no, yes, yes, yes, no, yes, no, no, yes, no, no, yes, yes, no, no, no, yes, no, no, yes, no…
$ Pclass <fct> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3, 2, 3, 3, 2, 2, 3, 1, 3, 3, 3, 1, 3, 3, 1, 1, 3, 2, 1, 1, 3, 3, 3, 3, 3, 2, 3, 2, 3, 3, 3, 3, 3, 3, 3, 3, 1, 2, 1, 1, 2, 3, 2, 3, 3…
$ Sex <fct> male, female, female, female, male, male, male, male, female, female, female, female, male, male, female, female, male, male, female, female, male, male, female, male, female, femal…
$ Age <dbl> 22.0, 38.0, 26.0, 35.0, 35.0, NA, 54.0, 2.0, 27.0, 14.0, 4.0, 58.0, 20.0, 39.0, 14.0, 55.0, 2.0, NA, 31.0, NA, 35.0, 34.0, 15.0, 28.0, 8.0, 38.0, NA, 19.0, NA, NA, 40.0, NA, NA, 66.…
$ Fare <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, 51.8625, 21.0750, 11.1333, 30.0708, 16.7000, 26.5500, 8.0500, 31.2750, 7.8542, 16.0000, 29.1250, 13.0000, 18.0000, 7.2250, 26.0000,…
$ FamSize <int> 1, 1, 0, 1, 0, 0, 0, 4, 2, 1, 2, 0, 0, 6, 0, 0, 5, 0, 1, 0, 0, 0, 0, 0, 4, 6, 0, 5, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 2, 1, 1, 1, 0, 3, 0, 0, 1, 0, 2, 1, 5, 0, 1, 1, 1, 0, 0, 0, 3, 7, 0…3.3 데이터 탐색
ggpairs(titanic1,
aes(colour = Survived)) + # Target의 범주에 따라 색깔을 다르게 표현
theme_bw()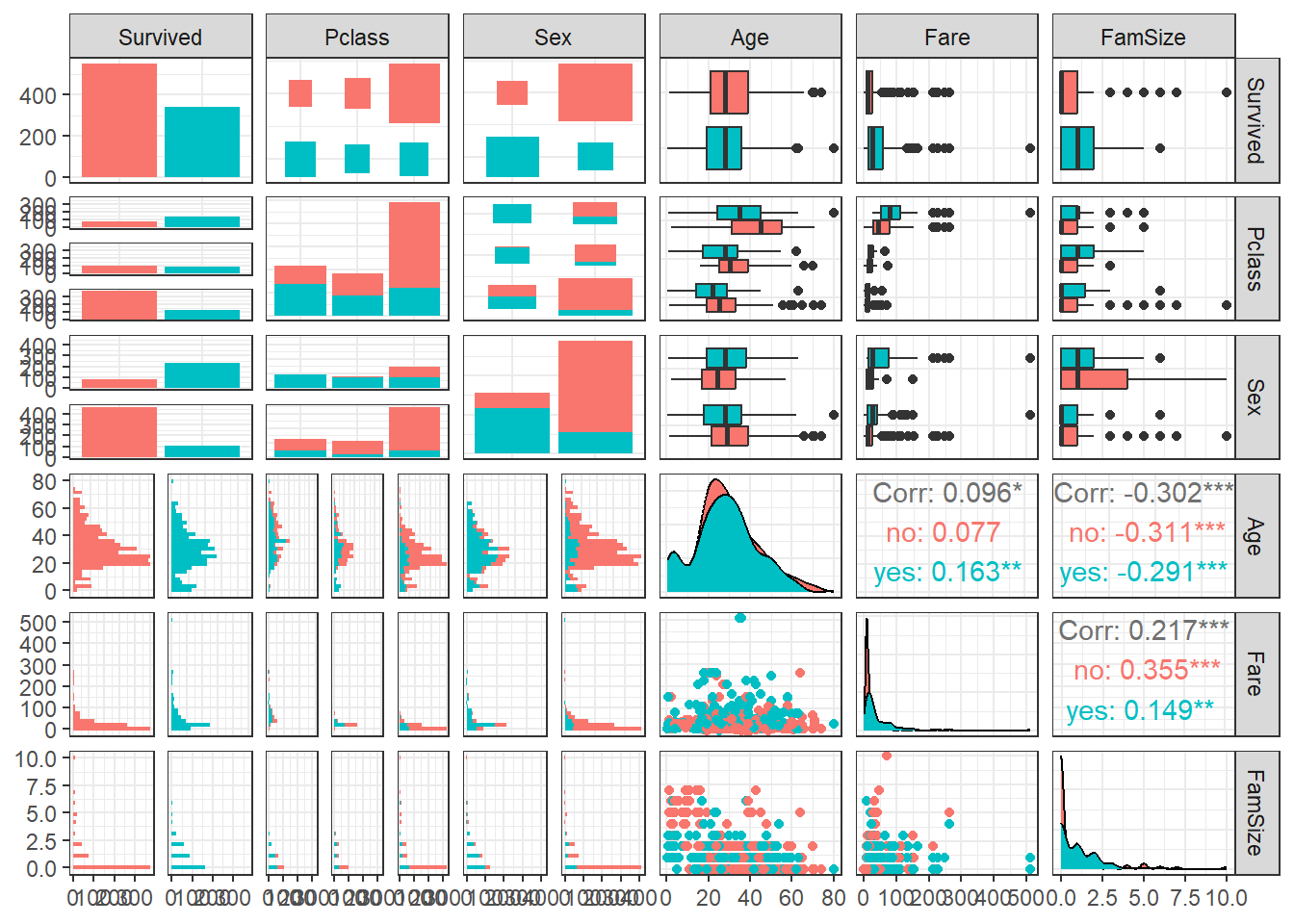
ggpairs(titanic1,
aes(colour = Survived, alpha = 0.8)) + # Target의 범주에 따라 색깔을 다르게 표현
scale_colour_manual(values = c("#00798c", "#d1495b")) + # 특정 색깔 지정
scale_fill_manual(values = c("#00798c", "#d1495b")) + # 특정 색깔 지정
theme_bw()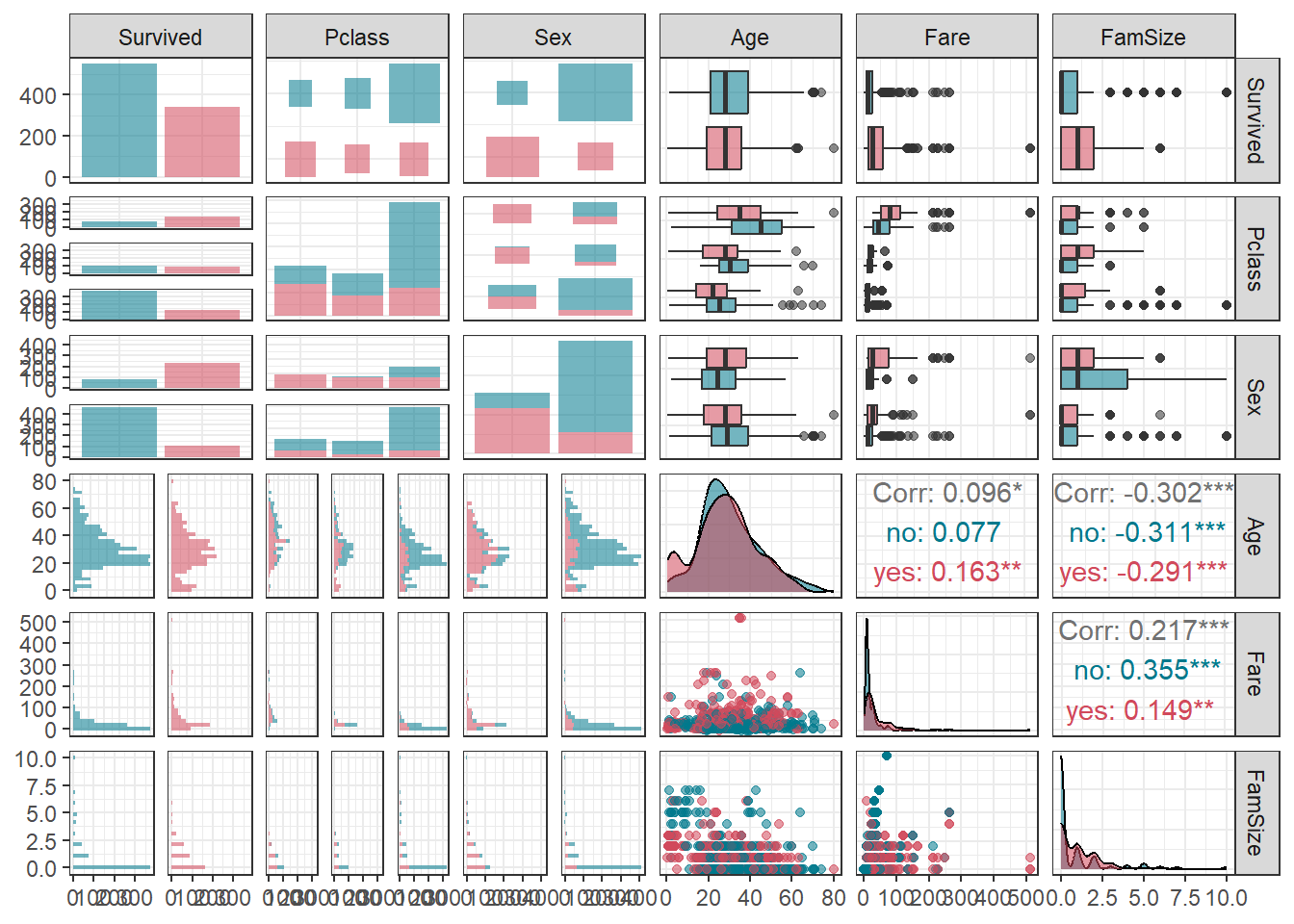
3.4 데이터 분할
# Partition (Training Dataset : Test Dataset = 7:3)
y <- titanic1$Survived # Target
set.seed(200)
ind <- createDataPartition(y, p = 0.7, list =T) # Index를 이용하여 7:3으로 분할
titanic.trd <- titanic1[ind$Resample1,] # Training Dataset
titanic.ted <- titanic1[-ind$Resample1,] # Test Dataset3.5 데이터 전처리 II
# Imputation
titanic.trd.Imp <- titanic.trd %>%
mutate(Age = replace_na(Age, mean(Age, na.rm = TRUE))) # 평균으로 결측값 대체
titanic.ted.Imp <- titanic.ted %>%
mutate(Age = replace_na(Age, mean(titanic.trd$Age, na.rm = TRUE))) # Training Dataset을 이용하여 결측값 대체
glimpse(titanic.trd.Imp) # 데이터 구조 확인Rows: 625
Columns: 6
$ Survived <fct> no, yes, yes, no, no, no, yes, yes, yes, yes, no, no, yes, no, yes, no, yes, no, no, no, yes, no, no, yes, yes, no, no, no, no, no, yes, no, no, no, yes, no, yes, no, no, no, yes, n…
$ Pclass <fct> 3, 3, 1, 3, 3, 3, 3, 2, 3, 1, 3, 3, 2, 3, 3, 2, 1, 3, 3, 1, 3, 3, 1, 1, 3, 2, 1, 1, 3, 3, 3, 3, 2, 3, 3, 3, 3, 3, 3, 3, 1, 1, 1, 3, 3, 1, 3, 1, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3, 1, 2, 3…
$ Sex <fct> male, female, female, male, male, male, female, female, female, female, male, female, male, female, female, male, male, female, male, male, female, male, male, female, female, male,…
$ Age <dbl> 22.00000, 26.00000, 35.00000, 35.00000, 29.93737, 2.00000, 27.00000, 14.00000, 4.00000, 58.00000, 39.00000, 14.00000, 29.93737, 31.00000, 29.93737, 35.00000, 28.00000, 8.00000, 29.9…
$ Fare <dbl> 7.2500, 7.9250, 53.1000, 8.0500, 8.4583, 21.0750, 11.1333, 30.0708, 16.7000, 26.5500, 31.2750, 7.8542, 13.0000, 18.0000, 7.2250, 26.0000, 35.5000, 21.0750, 7.2250, 263.0000, 7.8792,…
$ FamSize <int> 1, 0, 1, 0, 0, 4, 2, 1, 2, 0, 6, 0, 0, 1, 0, 0, 0, 4, 0, 5, 0, 0, 0, 1, 0, 0, 1, 1, 0, 2, 1, 1, 1, 0, 0, 1, 0, 2, 1, 5, 1, 1, 0, 7, 0, 0, 5, 0, 2, 7, 1, 0, 0, 0, 2, 0, 0, 0, 0, 0, 3…glimpse(titanic.ted.Imp) # 데이터 구조 확인Rows: 266
Columns: 6
$ Survived <fct> yes, no, no, yes, no, yes, yes, yes, yes, yes, no, no, yes, yes, no, yes, no, yes, yes, no, yes, no, no, no, no, no, no, yes, yes, no, no, no, no, no, no, no, no, no, no, yes, no, n…
$ Pclass <fct> 1, 1, 3, 2, 3, 2, 3, 3, 3, 2, 3, 3, 2, 2, 3, 2, 1, 3, 2, 3, 3, 2, 2, 3, 3, 3, 3, 1, 2, 2, 3, 3, 3, 3, 3, 2, 3, 2, 2, 2, 3, 3, 2, 1, 3, 1, 3, 2, 1, 3, 3, 3, 3, 3, 3, 3, 3, 1, 3, 1, 3…
$ Sex <fct> female, male, male, female, male, male, female, female, male, female, male, male, female, female, male, female, male, male, female, male, female, male, male, male, male, male, male,…
$ Age <dbl> 38.00000, 54.00000, 20.00000, 55.00000, 2.00000, 34.00000, 15.00000, 38.00000, 29.93737, 3.00000, 29.93737, 21.00000, 29.00000, 21.00000, 28.50000, 5.00000, 45.00000, 29.93737, 29.0…
$ Fare <dbl> 71.2833, 51.8625, 8.0500, 16.0000, 29.1250, 13.0000, 8.0292, 31.3875, 7.2292, 41.5792, 8.0500, 7.8000, 26.0000, 10.5000, 7.2292, 27.7500, 83.4750, 15.2458, 10.5000, 8.1583, 7.9250, …
$ FamSize <int> 1, 0, 0, 0, 5, 0, 0, 6, 0, 3, 0, 0, 1, 0, 0, 3, 1, 2, 0, 0, 6, 0, 0, 0, 0, 4, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 6, 2, 1, 0, 0, 1, 0, 2, 0, 0, 0, 0, 1, 0, 0, 1, 5, 2, 5, 0, 5, 0, 4, 0, 6…3.6 모형 훈련
Package "rpart"는 수정된 CART를 알고리듬으로 사용하며, CP (Complexity Parameter)를 이용하여 최적의 모형을 찾아낸다. CP는 최적의 나무 크기를 찾기 위한 모수로써, 노드를 분할할 때 분할 전과 비교하여 오분류율이 CP 값 이상으로 향상되지 않으면 분할을 멈춘다. 최적의 모형을 얻기 위해 필요한 CP는 Cross Validation (CV) 기법을 이용하여 얻을 수 있으며, 해당 Package에서는 기본값으로 10-Fold CV를 이용한다. 마지막으로, Package "rpart"는 가독성 좋은 그래프로 결과를 표현할 수 있어 의사결정나무를 시각화하기에 좋은 Package이다.
rpart(formula, data, method, ...)formula: Target과 예측 변수의 관계를 표현하기 위한 함수로써 일반적으로Target ~ 예측 변수의 형태로 표현한다.data:formula에 포함하고 있는 변수들의 데이터셋(Data Frame)method: Target이 범주형이면"class", 그렇지 않으면"anova"를 입력한다.
set.seed(200) # For Cross Validation (CV)
rContol <- rpart.control(xval = 5) # xval : xval-Fold CV
titanic.trd.rtree <- rpart(Survived ~ ., data = titanic.trd.Imp,
method = "class",
control = rContol)
summary(titanic.trd.rtree)Call:
rpart(formula = Survived ~ ., data = titanic.trd.Imp, method = "class",
control = rContol)
n= 625
CP nsplit rel error xerror xstd
1 0.40833333 0 1.0000000 1.0000000 0.05066228
2 0.03958333 1 0.5916667 0.5916667 0.04364821
3 0.03750000 3 0.5125000 0.5666667 0.04298062
4 0.01388889 4 0.4750000 0.5083333 0.04128694
5 0.01000000 7 0.4333333 0.5375000 0.04215843
Variable importance
Sex Fare Age Pclass FamSize
42 20 13 13 12
Node number 1: 625 observations, complexity param=0.4083333
predicted class=no expected loss=0.384 P(node) =1
class counts: 385 240
probabilities: 0.616 0.384
left son=2 (397 obs) right son=3 (228 obs)
Primary splits:
Sex splits as RL, improve=78.61042, (0 missing)
Pclass splits as RRL, improve=32.46336, (0 missing)
Fare < 51.2479 to the left, improve=29.66020, (0 missing)
Age < 6.5 to the right, improve=11.36591, (0 missing)
FamSize < 0.5 to the left, improve=11.20358, (0 missing)
Surrogate splits:
Fare < 56.9646 to the left, agree=0.674, adj=0.105, (0 split)
FamSize < 0.5 to the left, agree=0.666, adj=0.083, (0 split)
Age < 16.5 to the right, agree=0.642, adj=0.018, (0 split)
Node number 2: 397 observations, complexity param=0.0375
predicted class=no expected loss=0.1939547 P(node) =0.6352
class counts: 320 77
probabilities: 0.806 0.194
left son=4 (378 obs) right son=5 (19 obs)
Primary splits:
Age < 6.5 to the right, improve=11.762560, (0 missing)
Fare < 26.26875 to the left, improve= 9.994963, (0 missing)
Pclass splits as RLL, improve= 8.547643, (0 missing)
FamSize < 0.5 to the left, improve= 2.466746, (0 missing)
Node number 3: 228 observations, complexity param=0.03958333
predicted class=yes expected loss=0.2850877 P(node) =0.3648
class counts: 65 163
probabilities: 0.285 0.715
left son=6 (115 obs) right son=7 (113 obs)
Primary splits:
Pclass splits as RRL, improve=24.114900, (0 missing)
FamSize < 3.5 to the right, improve=14.973800, (0 missing)
Fare < 49.45 to the left, improve= 8.673891, (0 missing)
Age < 32.5 to the left, improve= 1.974352, (0 missing)
Surrogate splits:
Fare < 25.69795 to the left, agree=0.842, adj=0.681, (0 split)
Age < 29.96869 to the left, agree=0.667, adj=0.327, (0 split)
FamSize < 1.5 to the right, agree=0.566, adj=0.124, (0 split)
Node number 4: 378 observations
predicted class=no expected loss=0.1666667 P(node) =0.6048
class counts: 315 63
probabilities: 0.833 0.167
Node number 5: 19 observations
predicted class=yes expected loss=0.2631579 P(node) =0.0304
class counts: 5 14
probabilities: 0.263 0.737
Node number 6: 115 observations, complexity param=0.03958333
predicted class=no expected loss=0.4869565 P(node) =0.184
class counts: 59 56
probabilities: 0.513 0.487
left son=12 (19 obs) right son=13 (96 obs)
Primary splits:
FamSize < 3.5 to the right, improve=10.794200, (0 missing)
Fare < 24.80835 to the right, improve= 9.460870, (0 missing)
Age < 6.5 to the right, improve= 4.334995, (0 missing)
Surrogate splits:
Fare < 24.80835 to the right, agree=0.983, adj=0.895, (0 split)
Age < 38 to the right, agree=0.843, adj=0.053, (0 split)
Node number 7: 113 observations
predicted class=yes expected loss=0.05309735 P(node) =0.1808
class counts: 6 107
probabilities: 0.053 0.947
Node number 12: 19 observations
predicted class=no expected loss=0 P(node) =0.0304
class counts: 19 0
probabilities: 1.000 0.000
Node number 13: 96 observations, complexity param=0.01388889
predicted class=yes expected loss=0.4166667 P(node) =0.1536
class counts: 40 56
probabilities: 0.417 0.583
left son=26 (85 obs) right son=27 (11 obs)
Primary splits:
Age < 7 to the right, improve=2.6367200, (0 missing)
Fare < 15.3729 to the left, improve=1.3557420, (0 missing)
FamSize < 1.5 to the left, improve=0.1111111, (0 missing)
Node number 26: 85 observations, complexity param=0.01388889
predicted class=yes expected loss=0.4588235 P(node) =0.136
class counts: 39 46
probabilities: 0.459 0.541
left son=52 (52 obs) right son=53 (33 obs)
Primary splits:
Fare < 7.9021 to the right, improve=1.6989440, (0 missing)
Age < 29.96869 to the right, improve=1.0885760, (0 missing)
FamSize < 0.5 to the right, improve=0.2330413, (0 missing)
Surrogate splits:
FamSize < 0.5 to the right, agree=0.812, adj=0.515, (0 split)
Node number 27: 11 observations
predicted class=yes expected loss=0.09090909 P(node) =0.0176
class counts: 1 10
probabilities: 0.091 0.909
Node number 52: 52 observations, complexity param=0.01388889
predicted class=no expected loss=0.4615385 P(node) =0.0832
class counts: 28 24
probabilities: 0.538 0.462
left son=104 (30 obs) right son=105 (22 obs)
Primary splits:
Fare < 15.3729 to the left, improve=2.3310020, (0 missing)
Age < 23.5 to the left, improve=1.6011090, (0 missing)
FamSize < 0.5 to the left, improve=0.6930007, (0 missing)
Surrogate splits:
FamSize < 1.5 to the left, agree=0.731, adj=0.364, (0 split)
Age < 29.46869 to the left, agree=0.692, adj=0.273, (0 split)
Node number 53: 33 observations
predicted class=yes expected loss=0.3333333 P(node) =0.0528
class counts: 11 22
probabilities: 0.333 0.667
Node number 104: 30 observations
predicted class=no expected loss=0.3333333 P(node) =0.048
class counts: 20 10
probabilities: 0.667 0.333
Node number 105: 22 observations
predicted class=yes expected loss=0.3636364 P(node) =0.0352
class counts: 8 14
probabilities: 0.364 0.636 Result! 첫 번째 Table에서,
CP: Complexity Parameter로 Training Dataset에 대한 오분류율과 나무 크기에 대한 패널티를 이용하여 아래와 같이 계산한다. \[ \begin{align*} cp = \frac{p(\text{incorrect}_{l}) - p(\text{incorrect}_{l+1})}{n(\text{splits}_{l+1}) - n(\text{splits}_{l})}. \end{align*} \]- \(p(\text{incorrect}_{l})\) : 현재 Depth에서 오분류율
- \(n(\text{splits}_{l})\) :현재 Depth에서 분할 횟수
- \(p(\text{incorrect}_{l+1})\) : 다음 Depth에서 오분류율
- \(n(\text{splits}_{l+1})\) :다음 Depth에서 분할 횟수
예를 들어, 첫 번째 분할에서CP값은 다음과 같다.
\[ cp = \frac{1.00-0.592}{1-0} = 0.408 \]
nsplit: 분할 횟수rel error: 현재 Depth에서 잘못 분류된 Case들의 비율(오분류율)xerror: CV에 대한 오차xstd:xerror의 표준오차
두 번째 Table Variable importance은 변수 중요도에 대한 결과이며, 수치가 높을수록 중요한 변수임을 의미한다.
3.7 Tree Plot
3.7.1 “fancyRpartPlot”
fancyRpartPlot(titanic.trd.rtree) # Plot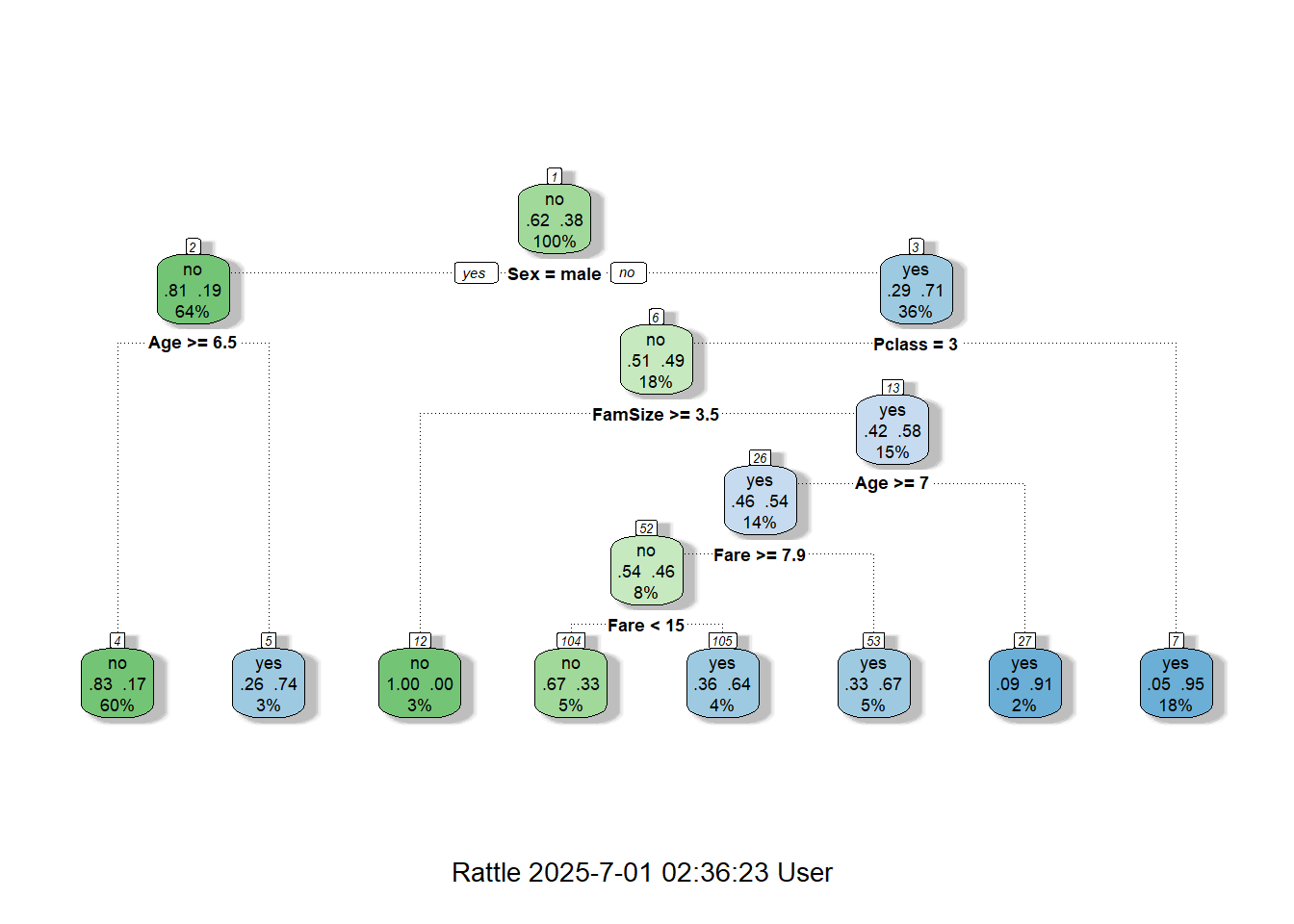
3.7.2 “visTree”
visTree(titanic.trd.rtree) # Network-based Plot 3.8 가지치기
가지치기(Pruning)는 생성된 가지를 잘라내어 모형을 단순화하는 과정을 의미한다. 의사결정나무 학습에서는 Training Dataset을 이용하여 노드에 대한 분할과정이 최대한 정확한 분류를 위해 계속 반복된다. 하지만, 과도한 반복은 많은 가지를 생성하게 되어 모형이 복잡해지고, 결과적으로 과대적합이 발생할 수 있다. 여기서 과대적합은 Training Dataset에 대해서는 정확하게 분류하지만 새로운 데이터셋인 Test Dataset에 대해서는 예측 성능이 현저히 떨어지는 현상을 의미한다. 따라서 의사결정나무는 가지치기를 통해 모형을 단순화하고 과대적합을 방지하는 과정이 필요하다.
Package "rpart"에서는 CP의 최적값을 이용하여 가지치기를 수행할 수 있다. 함수 rpart()를 이용하여 얻은 위의 결과를 기반으로 xerror가 최소가 되는 CP를 가지는 트리 모형을 생성한다.
table <- titanic.trd.rtree$cptable # CP Table
low.error <- which.min(table[ , "xerror"]) # min("xerror")에 해당하는 Index 추출
cp.best <- table[low.error, "CP"] # min("xerror")에 해당하는 CP 추출
# 가지치기 수행
titanic.trd.prune.rtree <- prune(titanic.trd.rtree, cp = cp.best) # prune(트리 모형, CP의 최적값)
titanic.trd.prune.rtree$cptable # Best 모형의 CP Table CP nsplit rel error xerror xstd
1 0.40833333 0 1.0000000 1.0000000 0.05066228
2 0.03958333 1 0.5916667 0.5916667 0.04364821
3 0.03750000 3 0.5125000 0.5666667 0.04298062
4 0.01388889 4 0.4750000 0.5083333 0.04128694fancyRpartPlot(titanic.trd.prune.rtree) # Plot 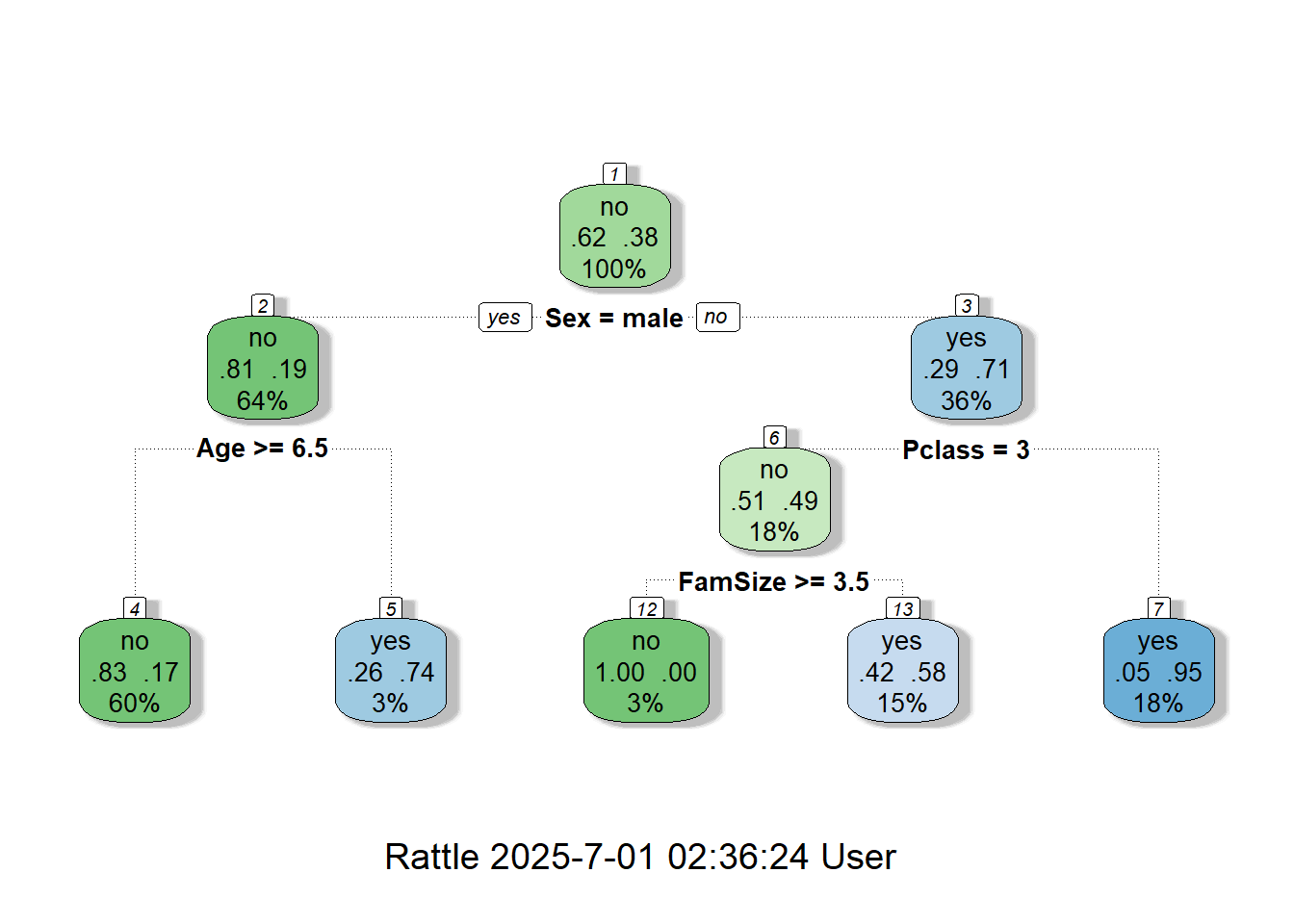
visTree(titanic.trd.prune.rtree) # Network-based Plot 3.9 모형 평가
Caution! 모형 평가를 위해 Test Dataset에 대한 예측 class/확률 이 필요하며, 함수 predict()를 이용하여 생성한다.
# 예측 class 생성
test.rtree.class <- predict(titanic.trd.prune.rtree,
newdata = titanic.ted.Imp[,-1], # Test Dataset including Only 예측 변수
type = "class") # 예측 class 생성
test.rtree.class %>%
as_tibble# A tibble: 266 × 1
value
<fct>
1 yes
2 no
3 no
4 yes
5 yes
6 no
7 yes
8 no
9 no
10 yes
# ℹ 256 more rows3.9.1 ConfusionMatrix
CM <- caret::confusionMatrix(test.rtree.class, titanic.ted.Imp$Survived,
positive = "yes") # confusionMatrix(예측 class, 실제 class, positive = "관심 class")
CMConfusion Matrix and Statistics
Reference
Prediction no yes
no 150 33
yes 14 69
Accuracy : 0.8233
95% CI : (0.7721, 0.8672)
No Information Rate : 0.6165
P-Value [Acc > NIR] : 1.974e-13
Kappa : 0.6127
Mcnemar's Test P-Value : 0.00865
Sensitivity : 0.6765
Specificity : 0.9146
Pos Pred Value : 0.8313
Neg Pred Value : 0.8197
Prevalence : 0.3835
Detection Rate : 0.2594
Detection Prevalence : 0.3120
Balanced Accuracy : 0.7956
'Positive' Class : yes
3.9.2 ROC 곡선
# 예측 확률 생성
test.rtree.prob <- predict(titanic.trd.prune.rtree,
newdata = titanic.ted.Imp[,-1], # Test Dataset including Only 예측 변수
type = "prob") # 예측 확률 생성
test.rtree.prob %>%
as_tibble# A tibble: 266 × 2
no yes
<dbl> <dbl>
1 0.0531 0.947
2 0.833 0.167
3 0.833 0.167
4 0.0531 0.947
5 0.263 0.737
6 0.833 0.167
7 0.417 0.583
8 1 0
9 0.833 0.167
10 0.0531 0.947
# ℹ 256 more rowstest.rtree.prob <- test.rtree.prob[,2] # "Survived = yes"에 대한 예측 확률
ac <- titanic.ted.Imp$Survived # Test Dataset의 실제 class
pp <- as.numeric(test.rtree.prob) # 예측 확률을 수치형으로 변환3.9.2.1 Package “pROC”
pacman::p_load("pROC")
rtree.roc <- roc(ac, pp, plot = T, col = "gray") # roc(실제 class, 예측 확률)
auc <- round(auc(rtree.roc), 3)
legend("bottomright", legend = auc, bty = "n")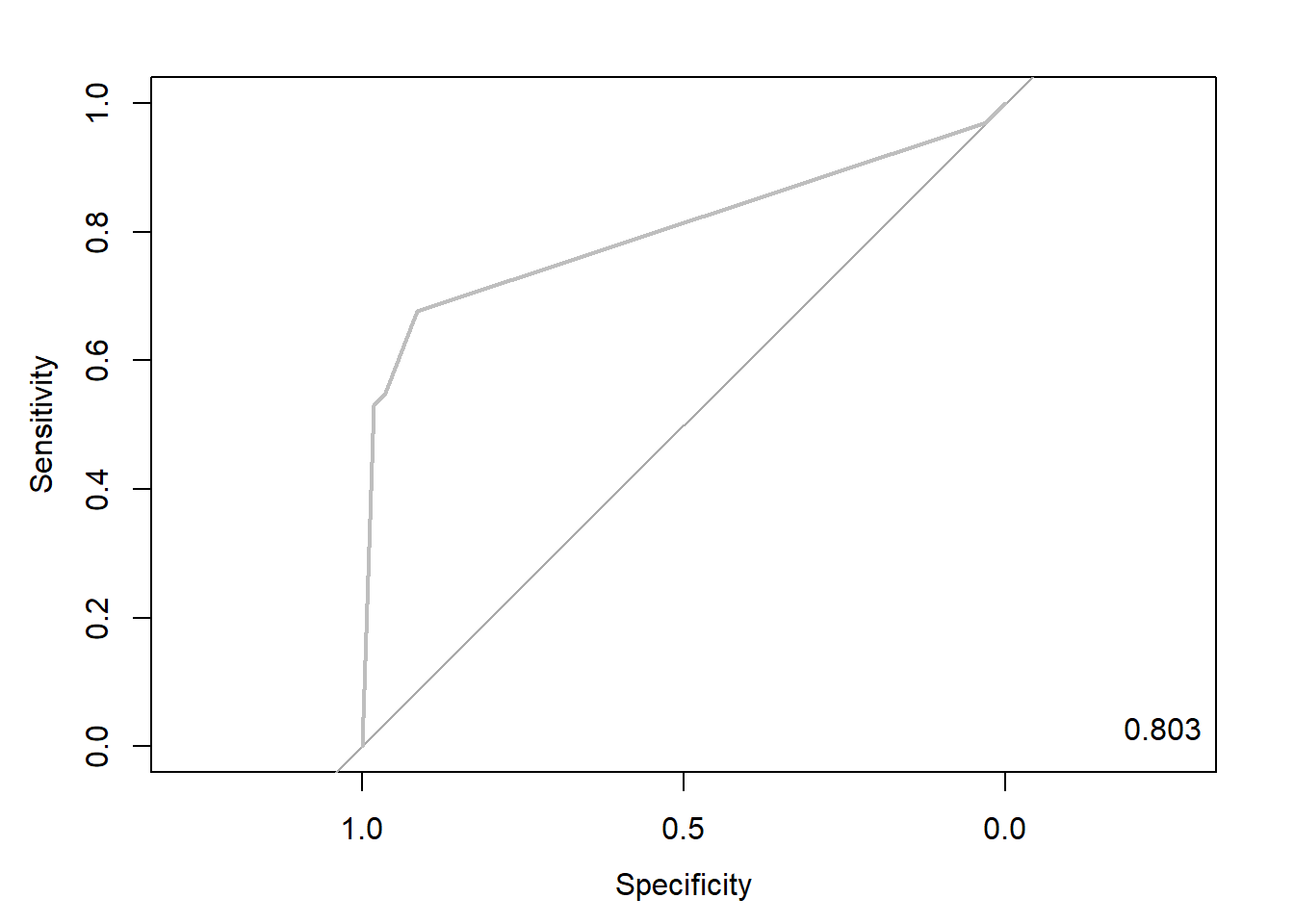
Caution! Package "pROC"를 통해 출력한 ROC 곡선은 다양한 함수를 이용해서 그래프를 수정할 수 있다.
# 함수 plot.roc() 이용
plot.roc(rtree.roc,
col="gray", # Line Color
print.auc = TRUE, # AUC 출력 여부
print.auc.col = "red", # AUC 글씨 색깔
print.thres = TRUE, # Cutoff Value 출력 여부
print.thres.pch = 19, # Cutoff Value를 표시하는 도형 모양
print.thres.col = "red", # Cutoff Value를 표시하는 도형의 색깔
auc.polygon = TRUE, # 곡선 아래 면적에 대한 여부
auc.polygon.col = "gray90") # 곡선 아래 면적의 색깔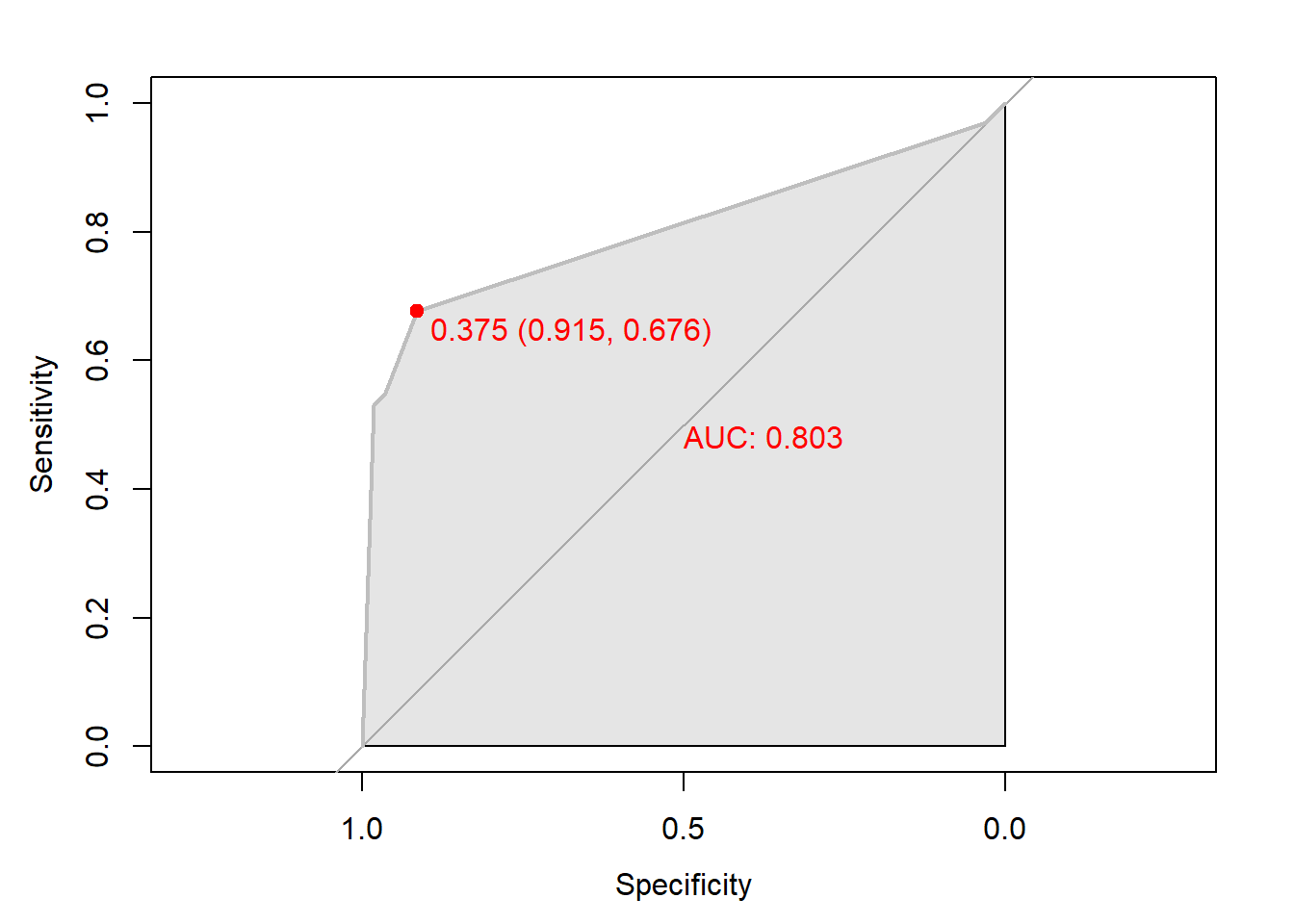
# 함수 ggroc() 이용
ggroc(rtree.roc) +
annotate(geom = "text", x = 0.9, y = 1.0,
label = paste("AUC = ", auc),
size = 5,
color="red") +
theme_bw()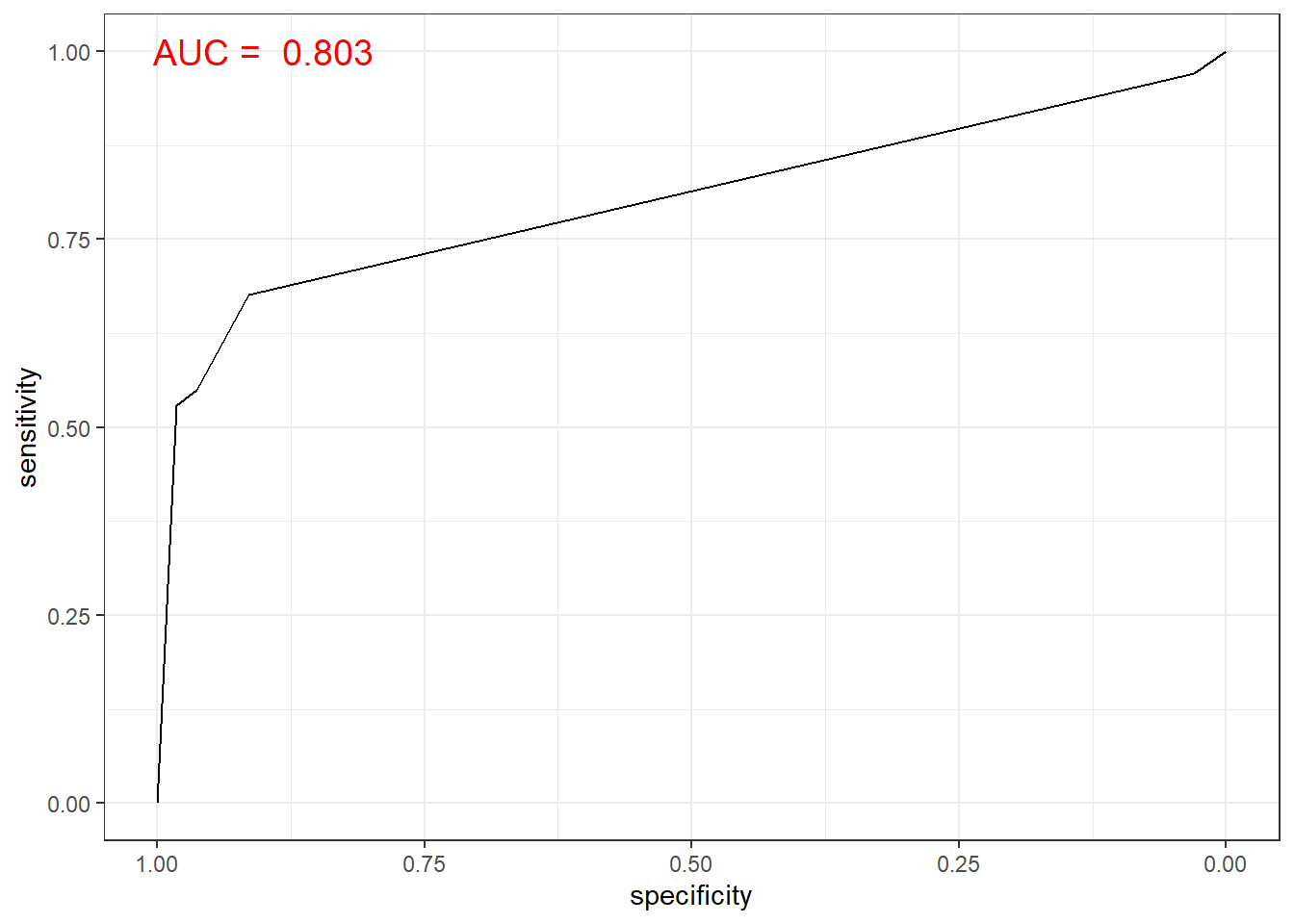
3.9.2.2 Package “Epi”
pacman::p_load("Epi")
# install_version("etm", version = "1.1", repos = "http://cran.us.r-project.org")
ROC(pp, ac, plot = "ROC") # ROC(예측 확률, 실제 class) 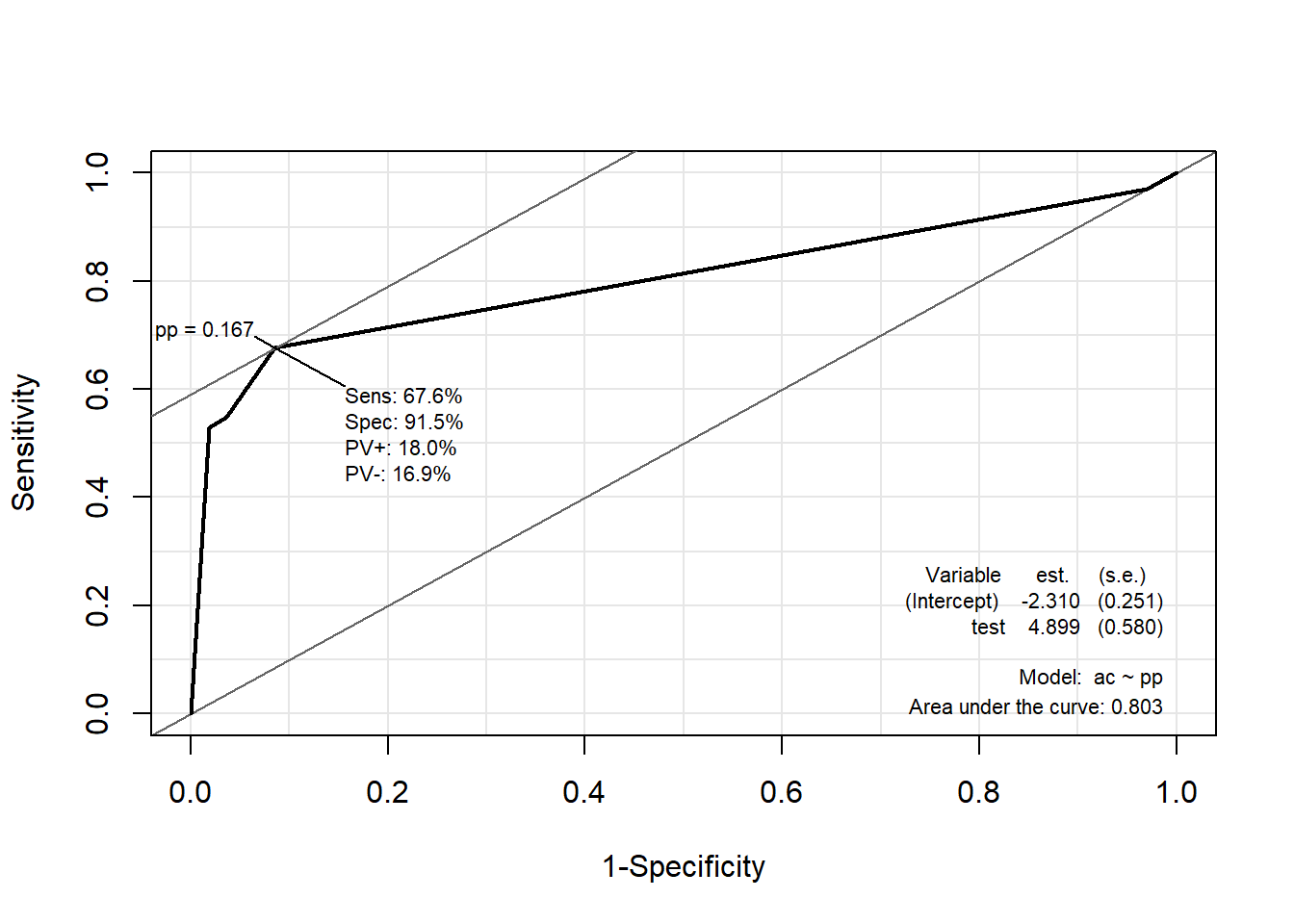
3.9.2.3 Package “ROCR”
pacman::p_load("ROCR")
rtree.pred <- prediction(pp, ac) # prediction(예측 확률, 실제 class)
rtree.perf <- performance(rtree.pred, "tpr", "fpr") # performance(, "민감도", "1-특이도")
plot(rtree.perf, col = "gray") # ROC Curve
perf.auc <- performance(rtree.pred, "auc") # AUC
auc <- attributes(perf.auc)$y.values
legend("bottomright", legend = auc, bty = "n")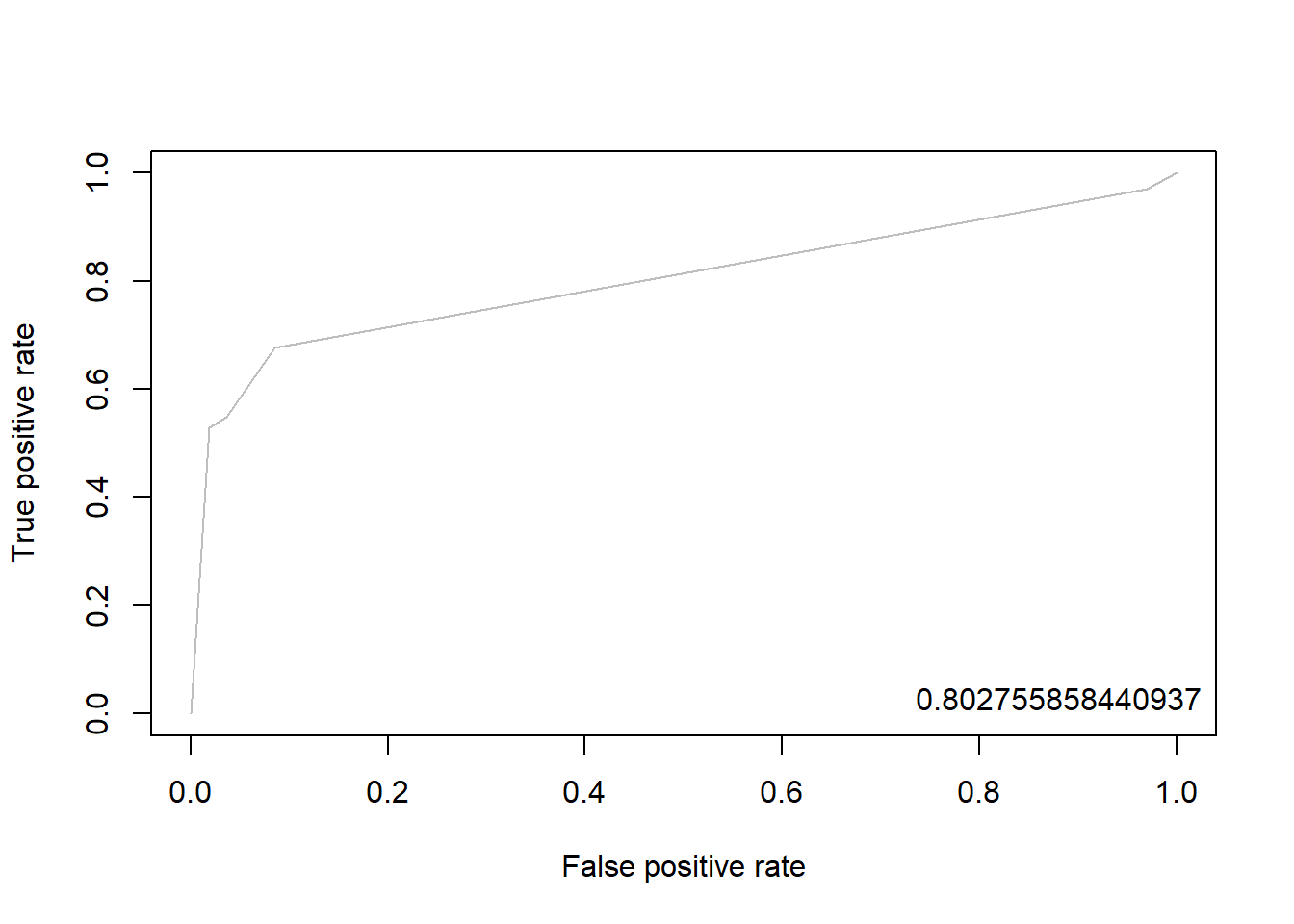
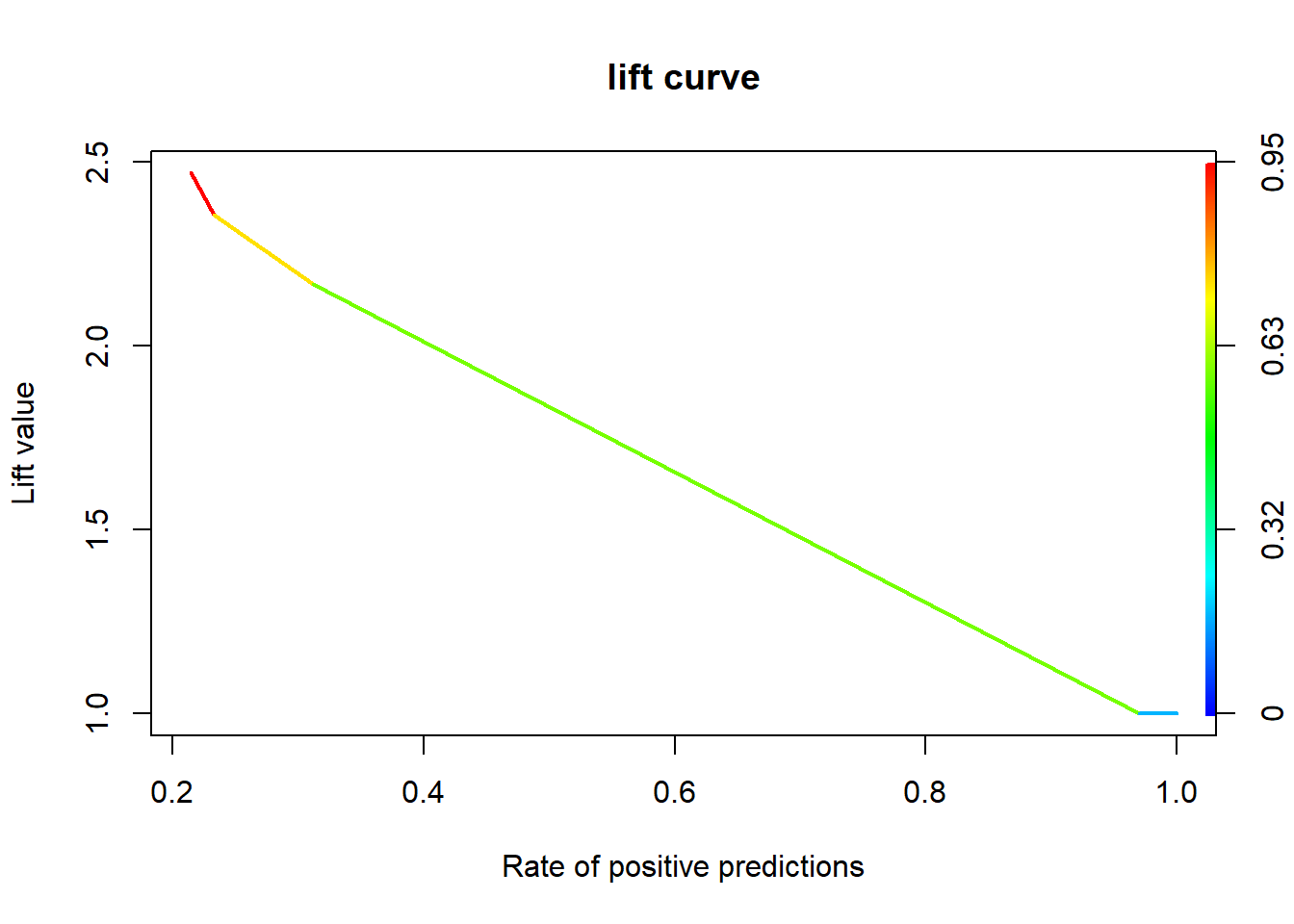
3.9.3 향상 차트
3.9.3.1 Package “ROCR”
rtree.perf <- performance(rtree.pred, "lift", "rpp") # Lift Chart
plot(rtree.perf, main = "lift curve",
colorize = T, # Coloring according to cutoff
lwd = 2)